computer graphics:计算机图形学学习

简简单单学个概念.

早期的OpenGL使用立即渲染模式（Immediate mode，也就是固定渲染管线），这个模式下绘制图形很方便。OpenGL的大多数功能都被库隐藏起来，开发者很少有控制OpenGL如何进行计算的自由。而开发者迫切希望能有更多的灵活性。随着时间推移，规范越来越灵活，开发者对绘图细节有了更多的掌控。立即渲染模式确实容易使用和理解，但是效率太低。因此从OpenGL3.2开始，规范文档开始废弃立即渲染模式，并鼓励开发者在OpenGL的核心模式(Core-profile)下进行开发，这个分支的规范完全移除了旧的特性。

当使用OpenGL的核心模式时，OpenGL迫使我们使用现代的函数。当我们试图使用一个已废弃的函数时，OpenGL会抛出一个错误并终止绘图。现代函数的优势是更高的灵活性和效率，然而也更难于学习。立即渲染模式从OpenGL实际运作中抽象掉了很多细节，因此它在易于学习的同时，也很难让人去把握OpenGL具体是如何运作的。现代函数要求使用者真正理解OpenGL和图形编程，它有一些难度，然而提供了更多的灵活性，更高的效率，更重要的是可以更深入的理解图形编程

使用GLAD和GLFW作为版本和窗口管理库.

glfwWindowShouldClose函数在我们每次循环的开始前检查一次GLFW是否被要求退出，如果是的话，该函数返回true，渲染循环将停止运行，之后我们就可以关闭应用程序。
glfwPollEvents函数检查有没有触发什么事件（比如键盘输入、鼠标移动等）、更新窗口状态，并调用对应的回调函数（可以通过回调方法手动设置）。
glfwSwapBuffers函数会交换颜色缓冲（它是一个储存着GLFW窗口每一个像素颜色值的大缓冲），它在这一迭代中被用来绘制，并且将会作为输出显示在屏幕上。

在OpenGL中，任何事物都在3D空间中，而屏幕和窗口却是2D像素数组，这导致OpenGL的大部分工作都是关于把3D坐标转变为适应你屏幕的2D像素。3D坐标转为2D坐标的处理过程是由OpenGL的图形渲染管线（Graphics Pipeline，大多译为管线，实际上指的是一堆原始图形数据途经一个输送管道，期间经过各种变化处理最终出现在屏幕的过程）管理的。图形渲染管线可以被划分为两个主要部分：第一部分把你的3D坐标转换为2D坐标，第二部分是把2D坐标转变为实际的有颜色的像素。

图形渲染管线接受一组3D坐标，然后把它们转变为你屏幕上的有色2D像素输出。图形渲染管线可以被划分为几个阶段，每个阶段将会把前一个阶段的输出作为输入。所有这些阶段都是高度专门化的（它们都有一个特定的函数），并且很容易并行执行。正是由于它们具有并行执行的特性，当今大多数显卡都有成千上万的小处理核心，它们在GPU上为每一个（渲染管线）阶段运行各自的小程序，从而在图形渲染管线中快速处理你的数据。这些小程序叫做着色器(Shader)。

有些着色器可以由开发者配置，因为允许用自己写的着色器来代替默认的，所以能够更细致地控制图形渲染管线中的特定部分了。因为它们运行在GPU上，所以节省了宝贵的CPU时间。OpenGL着色器是用OpenGL着色器语言(OpenGL Shading Language, GLSL)写成的

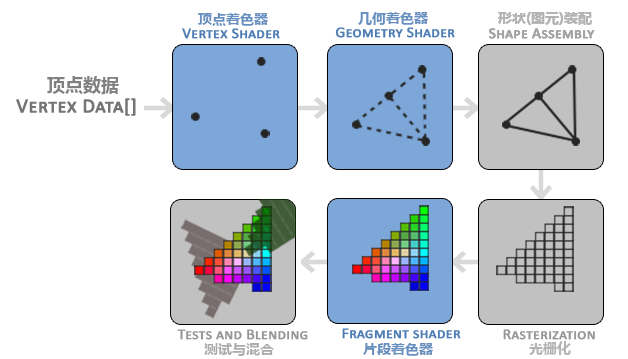
图形渲染管线包含很多部分，每个部分都将在转换顶点数据到最终像素这一过程中处理各自特定的阶段

图形渲染管线的第一个部分是顶点着色器(Vertex Shader)，它把一个单独的顶点作为输入。顶点着色器主要的目的是把3D坐标转为另一种3D坐标，同时顶点着色器允许我们对顶点属性进行一些基本处理

顶点着色器阶段的输出可以选择性地传递给几何着色器(Geometry Shader)。几何着色器将一组顶点作为输入，这些顶点形成图元，并且能够通过发出新的顶点来形成新的(或其他)图元来生成其他形状。在这个例子中，它从给定的形状中生成第二个三角形。

为了让OpenGL知道我们的坐标和颜色值构成的到底是什么，OpenGL需要你去指定这些数据所表示的渲染类型。我们是希望把这些数据渲染成一系列的点？一系列的三角形？还是仅仅是一个长长的线？做出的这些提示叫做图元(Primitive)，任何一个绘制指令的调用都将把图元传递给OpenGL。这是其中的几个：GL_POINTS、GL_TRIANGLES、GL_LINE_STRIP。

图元装配(Primitive Assembly)阶段将顶点着色器（或几何着色器）输出的所有顶点作为输入（如果是GL_POINTS，那么就是一个顶点），并将所有的点装配成指定图元的形状

图元装配阶段的输出会被传入光栅化阶段(Rasterization Stage)，这里它会把图元映射为最终屏幕上相应的像素，生成供片段着色器(Fragment Shader)使用的片段(Fragment)。在片段着色器运行之前会执行裁切(Clipping)。裁切会丢弃超出你的视图以外的所有像素，用来提升执行效率。

片段着色器的主要目的是计算一个像素的最终颜色，这也是所有OpenGL高级效果产生的地方。通常，片段着色器包含3D场景的数据（比如光照、阴影、光的颜色等等），这些数据可以被用来计算最终像素的颜色

在所有对应颜色值确定以后，最终的对象将会被传到最后一个阶段，我们叫做Alpha测试和混合(Blending)阶段。这个阶段检测片段的对应的深度（和模板(Stencil)）值（后面会讲），用它们来判断这个像素是其它物体的前面还是后面，决定是否应该丢弃。这个阶段也会检查alpha值（alpha值定义了一个物体的透明度）并对物体进行混合(Blend)。所以，即使在片段着色器中计算出来了一个像素输出的颜色，在渲染多个三角形的时候最后的像素颜色也可能完全不同

然而，对于大多数场合，我们只需要配置顶点和片段着色器就行了。几何着色器是可选的，通常使用它默认的着色器就行了。

在现代OpenGL中，我们必须定义至少一个顶点着色器和一个片段着色器（因为GPU中没有默认的顶点/片段着色器）。出于这个原因，刚开始学习现代OpenGL的时候可能会非常困难，因为在你能够渲染自己的第一个三角形之前已经需要了解一大堆知识了。在本节结束你最终渲染出你的三角形的时候，你也会了解到非常多的图形编程知识。

OpenGL是一个3D图形库，所以在OpenGL中我们指定的所有坐标都是3D坐标（x、y和z）。OpenGL不是简单地把所有的3D坐标变换为屏幕上的2D像素；OpenGL仅当3D坐标在3个轴（x、y和z）上-1.0到1.0的范围内时才处理它。所有在这个范围内的坐标叫做标准化设备坐标(Normalized Device Coordinates)，此范围内的坐标最终显示在屏幕上（在这个范围以外的坐标则不会显示）。

通常深度可以理解为z坐标，它代表一个像素在空间中和你的距离，如果离你远就可能被别的像素遮挡，你就看不到它了，它会被丢弃，以节省资源。

通过使用由glViewport函数提供的数据，进行视口变换(Viewport Transform)，标准化设备坐标(Normalized Device Coordinates)会变换为屏幕空间坐标(Screen-space Coordinates)。所得的屏幕空间坐标又会被变换为片段输入到片段着色器中。定义这样的顶点数据以后，我们会把它作为输入发送给图形渲染管线的第一个处理阶段：顶点着色器。它会在GPU上创建内存用于储存我们的顶点数据，还要配置OpenGL如何解释这些内存，并且指定其如何发送给显卡。顶点着色器接着会处理我们在内存中指定数量的顶点。

我们通过顶点缓冲对象(Vertex Buffer Objects, VBO)管理这个内存，它会在GPU内存（通常被称为显存）中储存大量顶点。使用这些缓冲对象的好处是我们可以一次性的发送一大批数据到显卡上，而不是每个顶点发送一次。从CPU把数据发送到显卡相对较慢，所以只要可能我们都要尝试尽量一次性发送尽可能多的数据。当数据发送至显卡的内存中后，顶点着色器几乎能立即访问顶点，这是个非常快的过程。

unsigned int VBO;
glGenBuffers(1, &VBO);
glBindBuffer(GL_ARRAY_BUFFER, VBO); 
glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);

现在我们已经把顶点数据储存在显卡的内存中，用VBO这个顶点缓冲对象管理。下面我们会创建一个顶点着色器和片段着色器来真正处理这些数据。。

顶点着色器(Vertex Shader)是几个可编程着色器中的一个。如果我们打算做渲染的话，现代OpenGL需要我们至少设置一个顶点和一个片段着色器。

#version 330 core
layout (location = 0) in vec3 aPos;

void main()
{
    gl_Position = vec4(aPos.x, aPos.y, aPos.z, 1.0);
}

使用in关键字，在顶点着色器中声明所有的输入顶点属性(Input Vertex Attribute)。现在我们只关心位置(Position)数据，所以我们只需要一个顶点属性。GLSL有一个向量数据类型，它包含1到4个float分量，包含的数量可以从它的后缀数字看出来

每个顶点都有一个3D坐标，我们就创建一个vec3输入变量aPos。我们同样也通过layout (location = 0)设定了输入变量的位置值(Location)你后面会看到为什么我们会需要这个位置值.

写好glsl后,首先创建一个着色器对象，注意还是用ID来引用的。所以我们储存这个顶点着色器为unsigned int，然后用glCreateShader创建这个着色器

GAMES101

转换

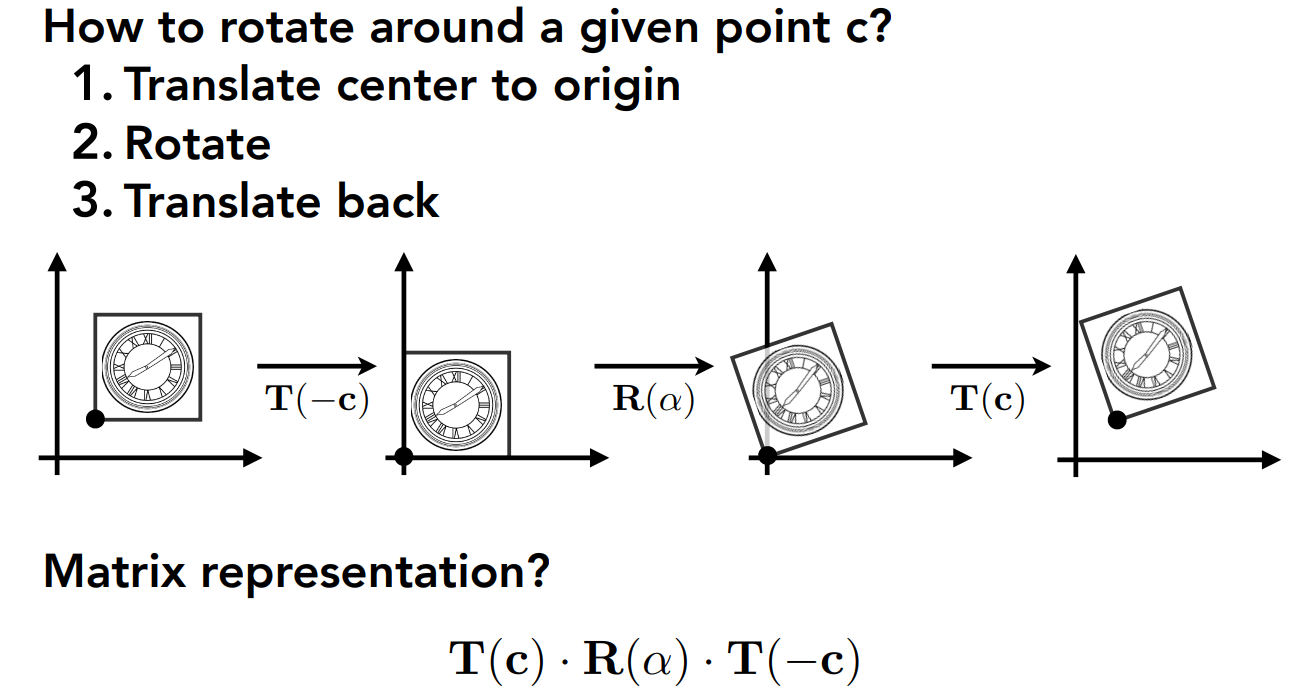
使用homegeneous coordinates,因为Translation cannot be represented in matrix form

assignment

HW0

学习Eigen库,二维和三维的空间变换,都可以拆成旋转,放缩和平移,但是平移无法使用与坐标维数相同的转换矩阵,可以通过homogeneous coordinates.

HW1

观测转换,视图和投影转换. 投影转换又可以分为正交和透视投影.

view transformation就是相机的摆放,包括位置,朝向和向上的方向.

又叫做ModelView Transformation.

相当于将相机连着物体一起做变换,使得相机朝着-Z,位置在原点,向上方向在Y.

一般做view transformation就是先平移后旋转.

然后做投影,也就是将3D变为2D,先做透视再做正交. 做透视因为符合视觉系统,做正交将物体归一化并放在中心.

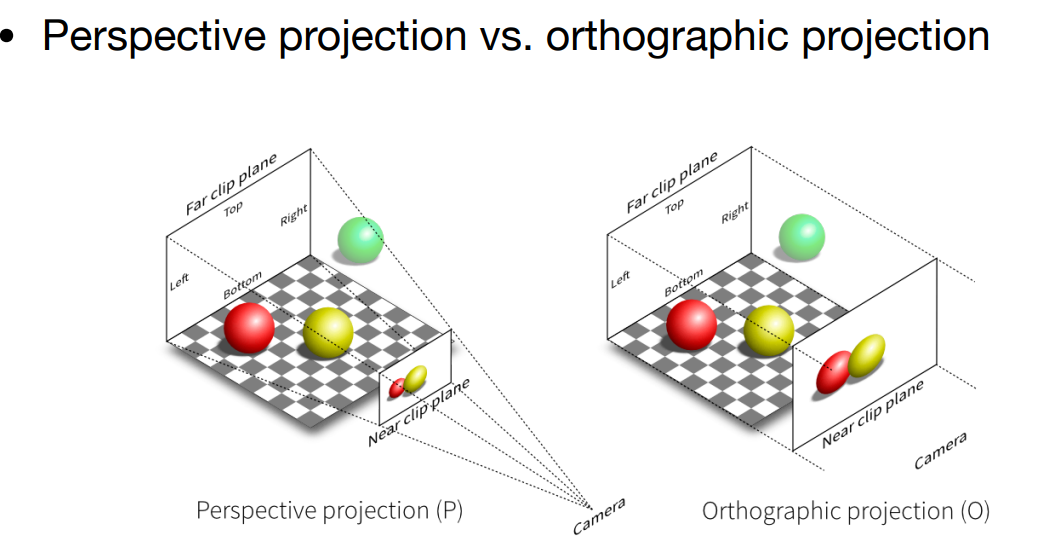
做正交矩阵如下.

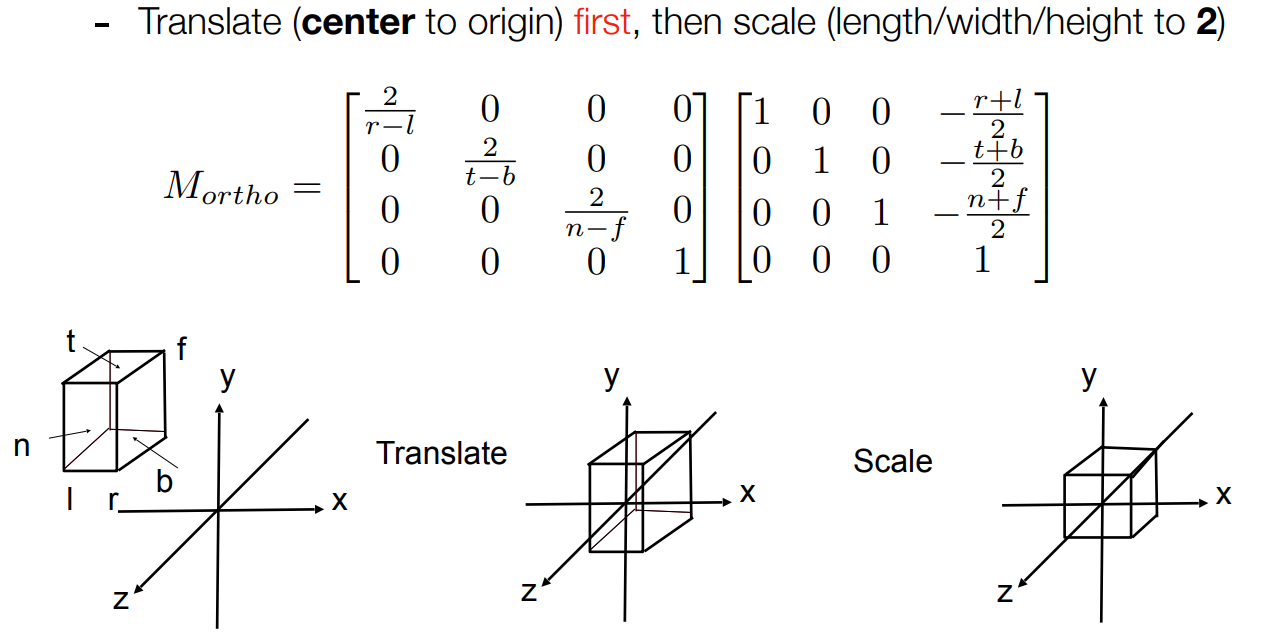
做投影如下,

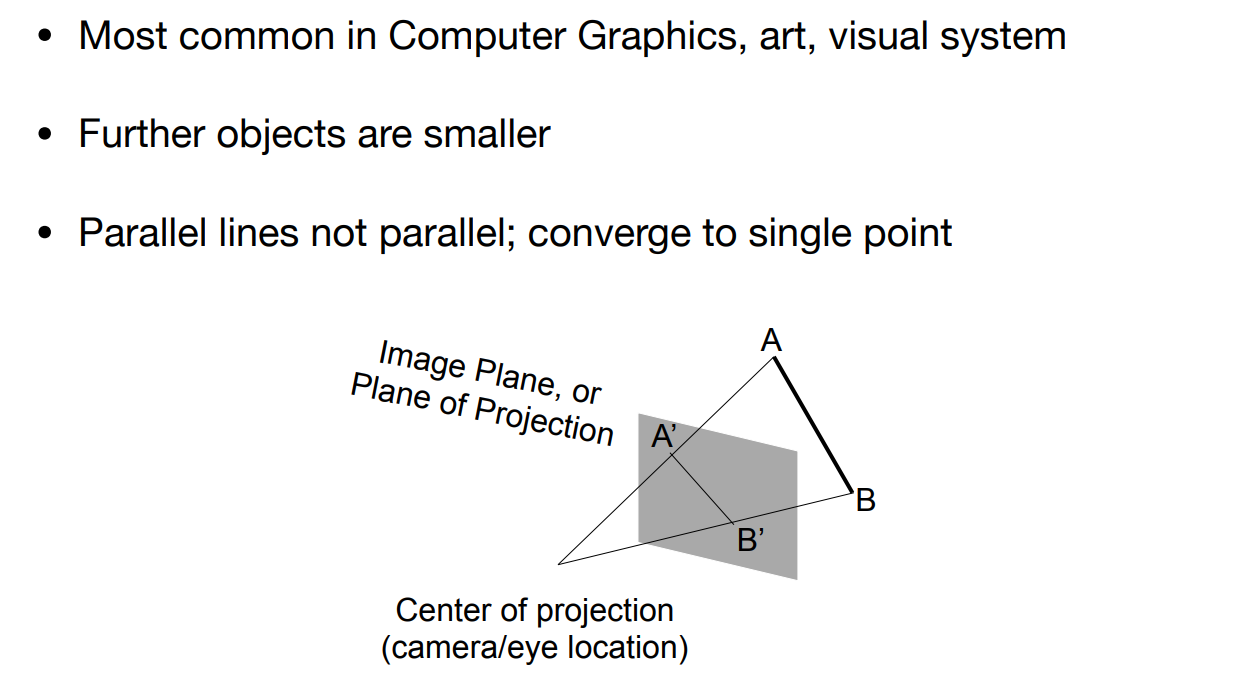
重点是关于透视矩阵的推理,首先因为等比例的坐标缩放,

$\begin{pmatrix}x\\y\\z\\1\end{pmatrix}\Rightarrow\begin{pmatrix}nx/z\\ny/z\\\text{unknown}\\1\end{pmatrix}\overset{\text{mult by z}}{\operatorname*{==}}\begin{pmatrix}nx\\ny\\\text{still unknown}\\z\end{pmatrix}$

这样就知道透视投影矩阵的三行信息

$M_{persp\to ortho}^{(4\times4)}\begin{pmatrix}x\\y\\z\\1\end{pmatrix}=\begin{pmatrix}nx\\ny\\\text{unknown}\\z\end{pmatrix} \\ M_{persp\to ortho}=\begin{pmatrix}n&0&0&0\\0&n&0&0\\?&?&?&?\\0&0&1&0\end{pmatrix}$

此外,有两点:在near plane也就是投影到的平面上的坐标经过这个矩阵转换后依然不变,而far plane上的坐标经过透视投影后z坐标不变.

对于near plane(x,y,n,1),由于转换后坐标相同得到(nx,ny,n^2^,n).

$\begin{pmatrix}0&0&A&B\end{pmatrix}\begin{pmatrix}x\\y\\n\\1\end{pmatrix}=n^2$

所以第三行的值必须是(0,0,A,B).即有An+B=n^2^.

假设far plane上的一个点坐标是(x,y,f,1),也有Af+B=f^2^.解得

$\begin{aligned}An+B&=n^2\\Af+B&=f^2\end{aligned}\quad\begin{array}{c}A=n+f\\B=-nf\end{array}$

所以透视矩阵如下,其中n是near plane上的点的z坐标,f是随便一个点的z坐标.

$M_{persp\to ortho}=\begin{pmatrix}n&0&0&0\\0&n&0&0\\0&0&n+f&-nf\\0&0&1&0\end{pmatrix}$

有了透视矩阵后,正交矩阵比较简单.在进行投影时先透视后正交就得到投影矩阵了. 如果有了near plane的四个点坐标就方便进行视口变换,或者通过fovY和aspect ratio,前者是一个角度,可以通过这个角度知道视点与near plane平面的距离,aspect ratio是平面宽度/高度.

$\tan\frac{fovY}2=\frac t{|n|}\\aspect=\frac rt$

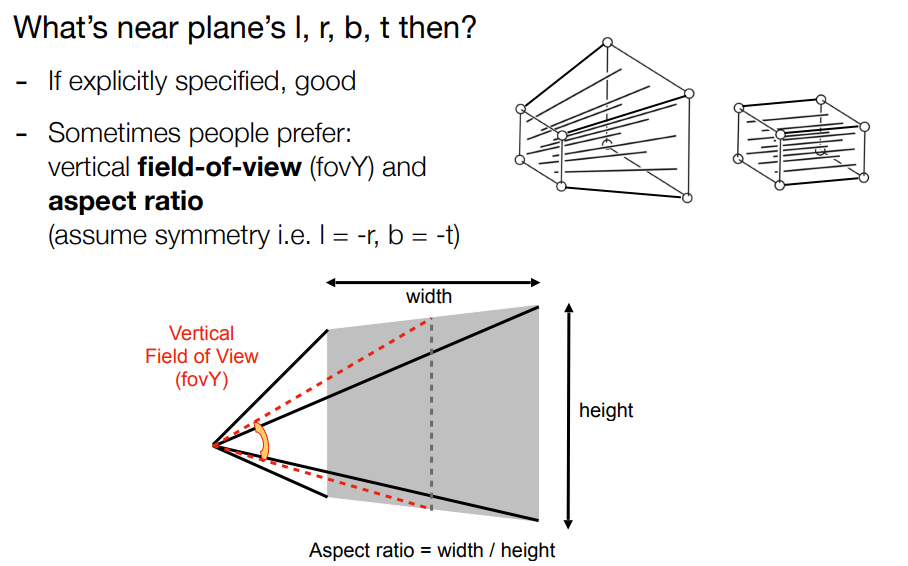
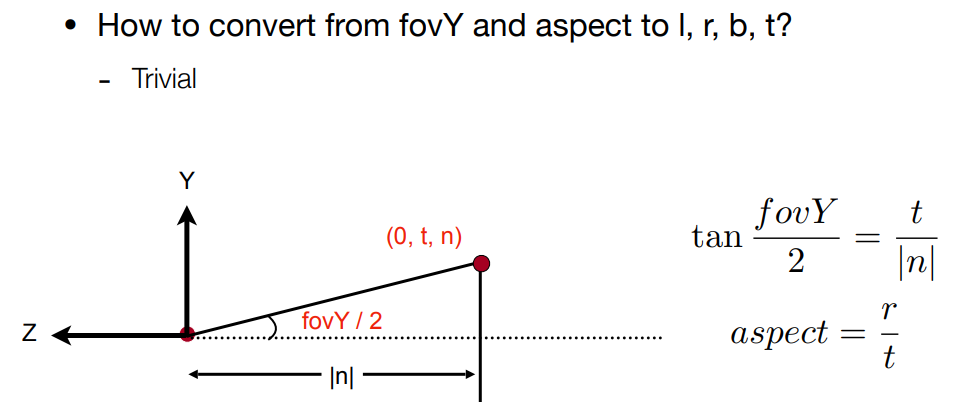
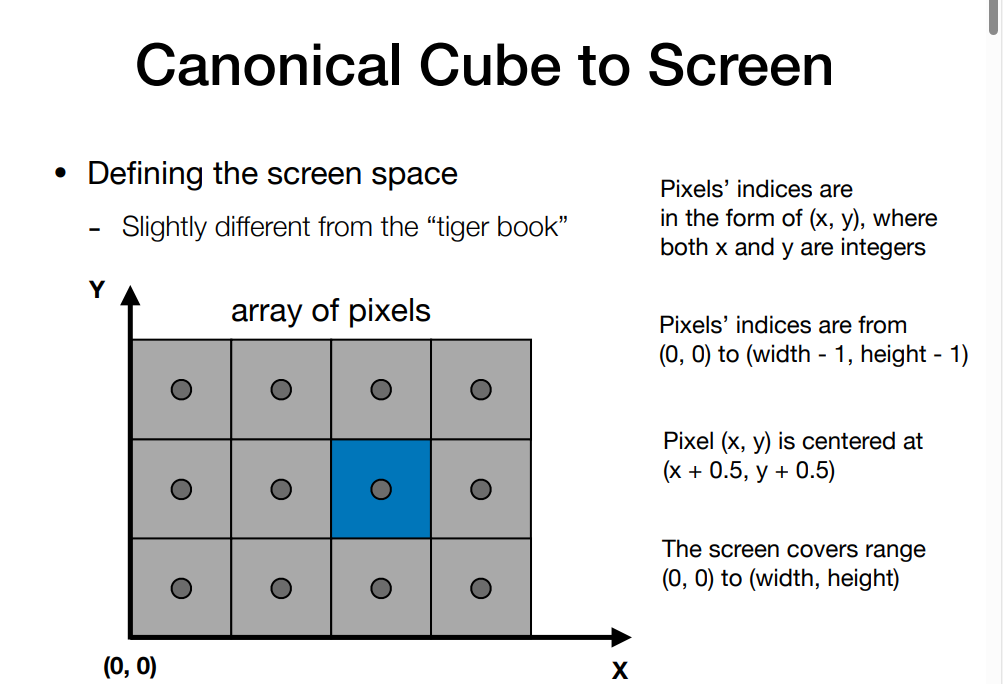
在图形学的MVP(model transformation,view transformation,project transformation)之后,得到了规范的2D投影.然后需要将规范的cube转到screen上(视口转换),screen就是一个pixel的数组,大小是分辨率.raster就是screen.

因为坐标已经归一到[-1,1],再转到[0,width]x[0,height],线性转换即可.z坐标不用管

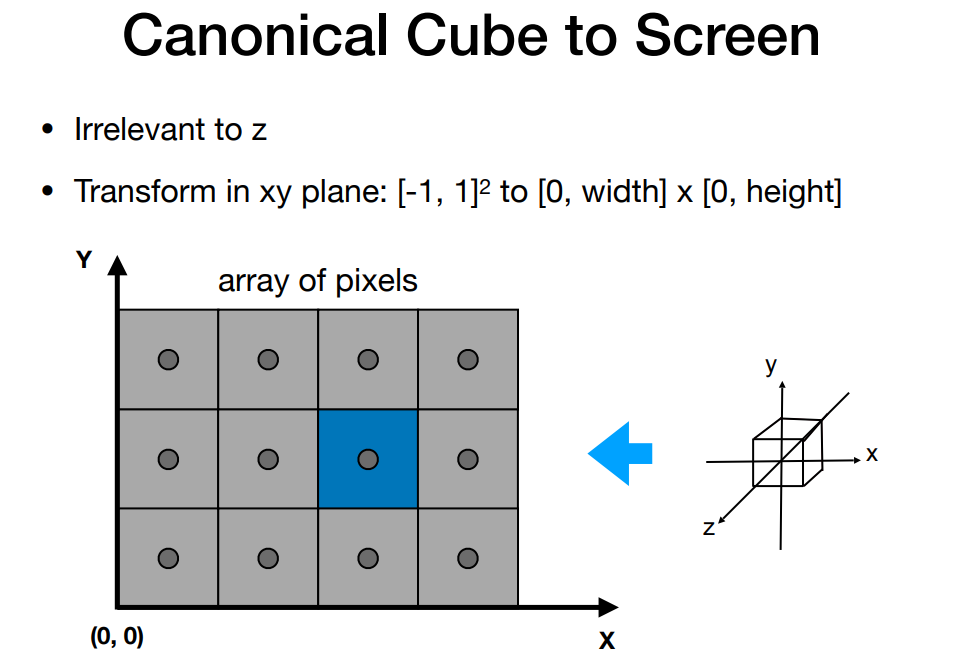
提升题

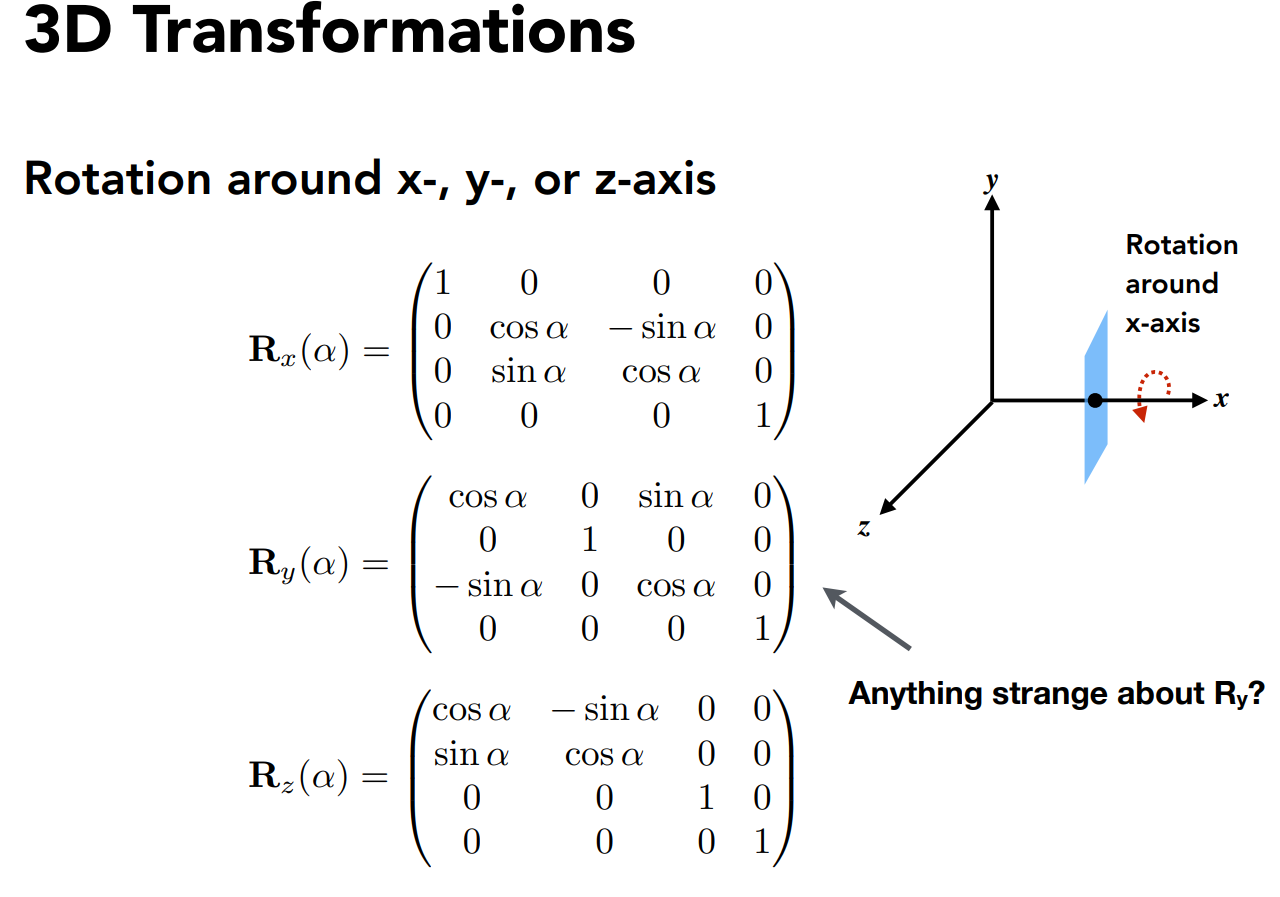
绕任意过原点的轴的旋转变换矩阵。

HW2

上面的就画出了一个线框,但是为了画出完整三角形,线框里的值还需要光栅化.首先需要判定点是否在线框内,涉及到cross products和使用bounding box. 如果在内部,还需要判断内部点的深度.如果当前点更靠近相机,设置像素颜色并更新depth buffer.

首先bounding box比较简单,直接获得x,y的最小值最大值即可 .

判定点是否在三角形内,在三角形内还需要使用重心插值得到z-buffering,这里越小表示越近,如果更小就设置颜色.

for (int x = floor(lb_x); x < ceil(rt_x); x++) {
        for (int y = floor(lb_y); y < ceil(rt_y); y++) {
            if (insideTriangle(x+0.5, y+0.5, t.v)) {
                auto[alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
                float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                z_interpolated *= w_reciprocal;
                int index = get_index(x, y);
                if (z_interpolated < depth_buf[index]) {
                    depth_buf[index] = z_interpolated;
                    set_pixel(Vector3f(x, y, 1.0f), t.getColor());

                }

            }
        }
    }

为了解决锯齿问题(antialiasing),可以先进行卷积,也可以进行supersamping,这里使用super-samping,对每个像素进行2x2采样.

方法是

Take NxN samples in each pixel.
Average the NxN samples “inside” each pixel

具体做的时候针对每个pixel,需要保存两个 sample list里面存着周围几个元素的颜色与depth. 然后算color的均值.

super-sampling时,会对一个像素结合多个强度(颜色),也就是均值.采样的值太大图像会变糊.

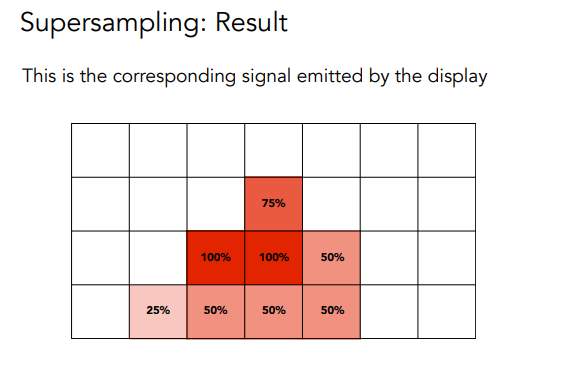
HW3

之前涉及到了MVP,视口转换以及Raster、=-Z-buffer. 现在到了shading

Shading:The process of applying a material to an object.The darkening or coloring of an illustration or diagram with parallel lines or a block of color

这里Shading介绍了Blinn-Phong反射模型,包括漫反射,高光反射和环境光.

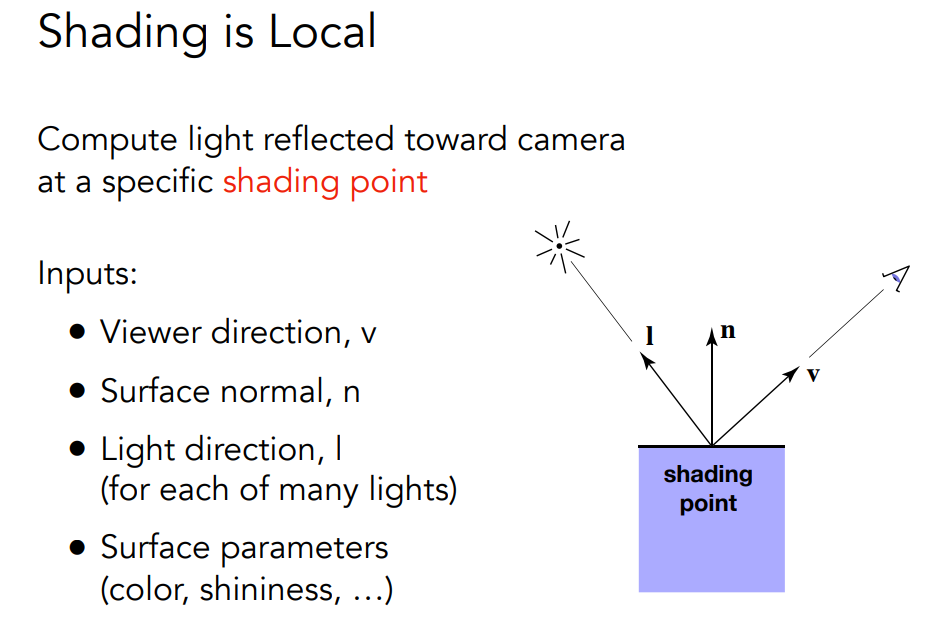
漫反射

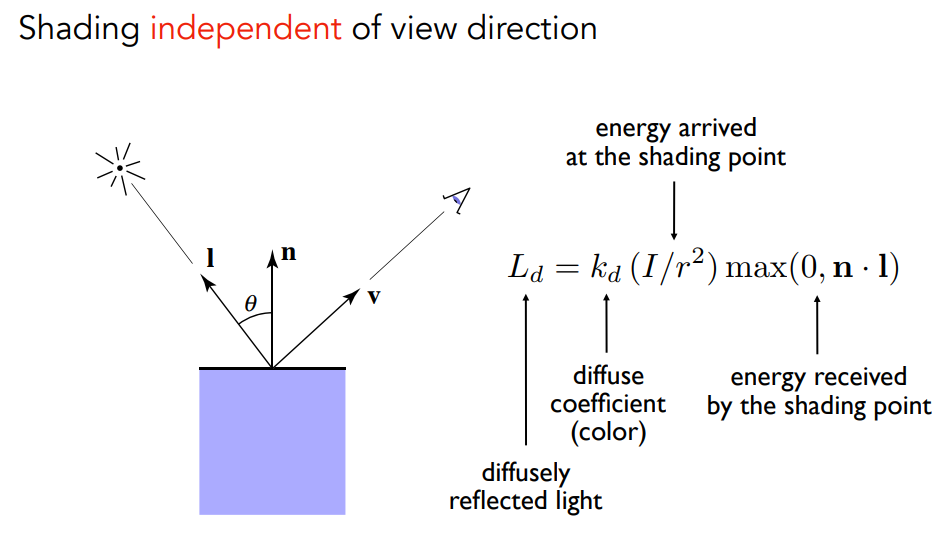与看的方向无关,与距离和入射角度有关. kd对漫反射影响如下.

高光反射

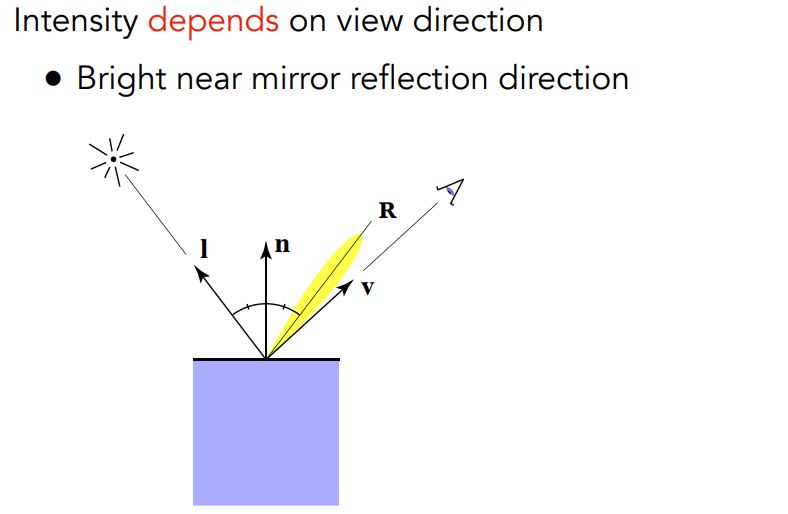
与看的角度有关,角度跟入射角相等时最大.

半程向量就是以l和v向量为边的中线,而p叫做cosine power plots,越大相同角度下越小.

ks和p对高光反射影响如下

环境光

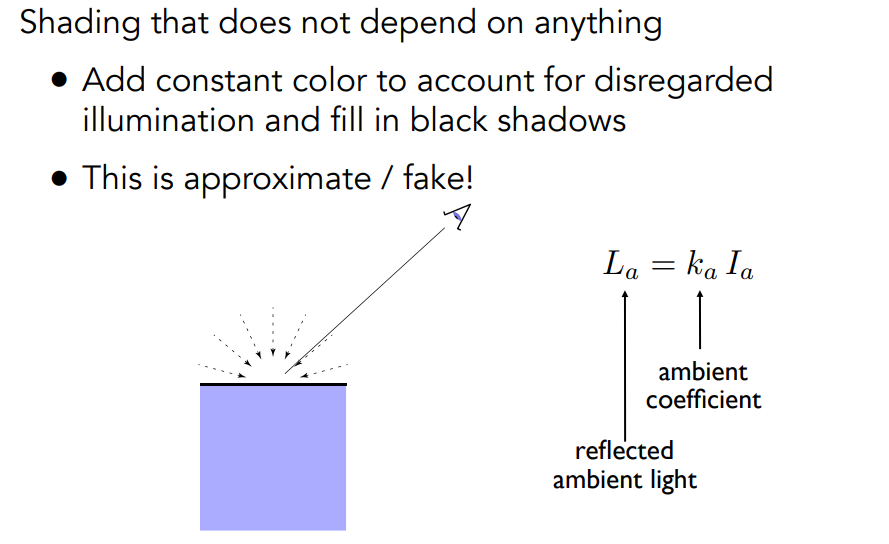
不依赖于任何东西,相当于加点环境噪音

所以最后在Blinn-Phong反射模型中,着色如下

此外shading还跟着色频率有关,分为三种类型,包括flat shading,gouraud shading,Phong shading

flat shading

Triangle face is flat — one normal vector
Not good for smooth surfaces

对于每个三角形做shading,每个三角形就一个normal vector

gouraud shading

Interpolate colors from vertices across triangle
Each vertex has a normal vector

对于每个vertex做,每个vertex搞出来一个normal vector.

Phong shading

Interpolate normal vectors across each triangle
Compute full shading model at each pixel

对于每个pixel做.

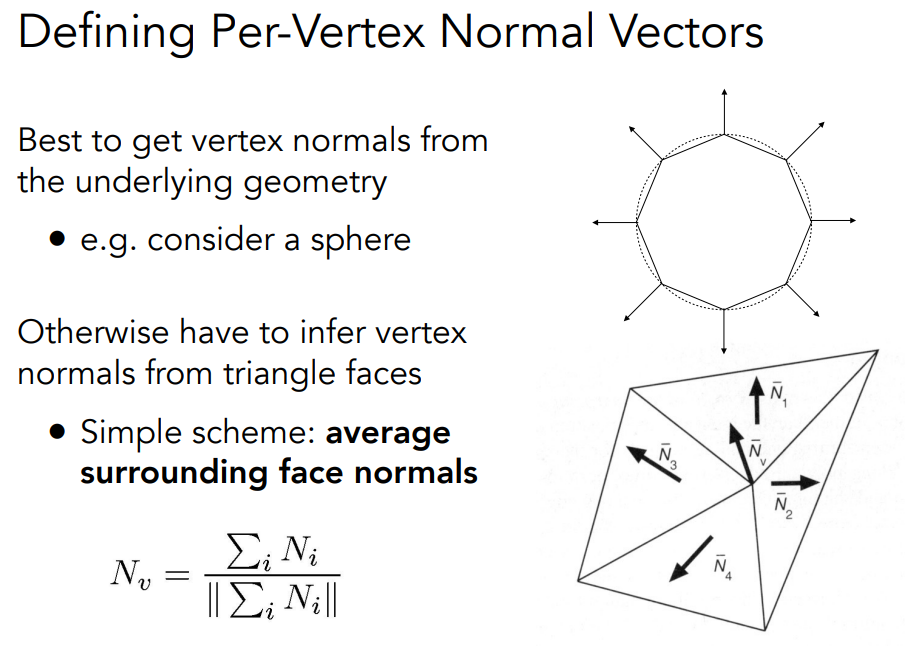
重心插值

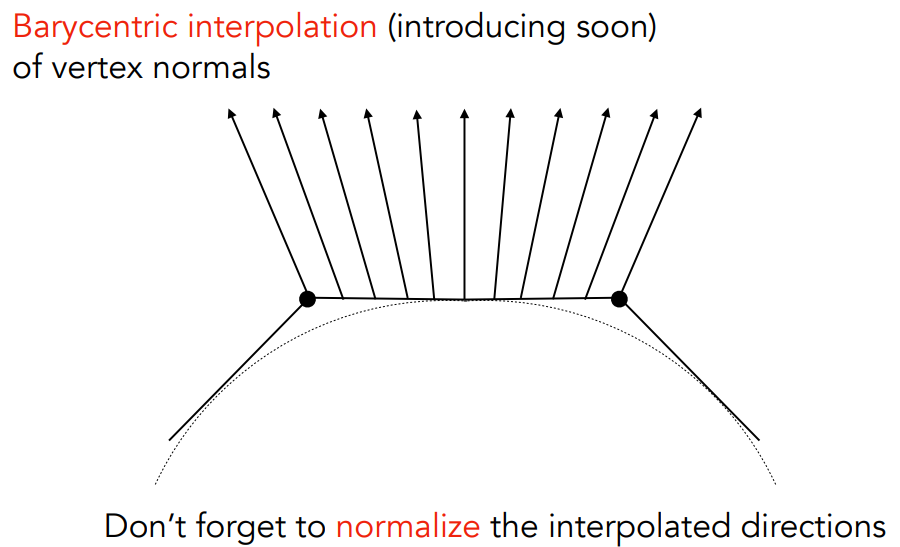
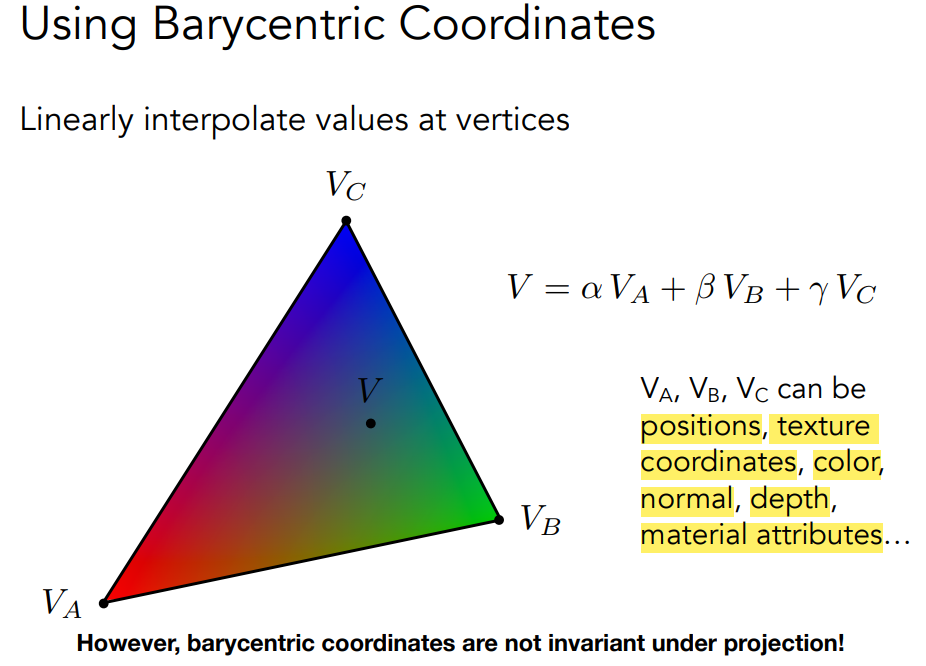
重心坐标系是指平面上任意一点可以用三角形的三个顶点的坐标的线性组合表示,其中三个系数的和为1。

Texture mapping

apply textures = sampling

应用texture的方法,对于每个screen的点,得到对应的texture coords(u,v)然后sample出一个颜色,设置这个颜色为点的颜色,常作为漫反射的系数kd

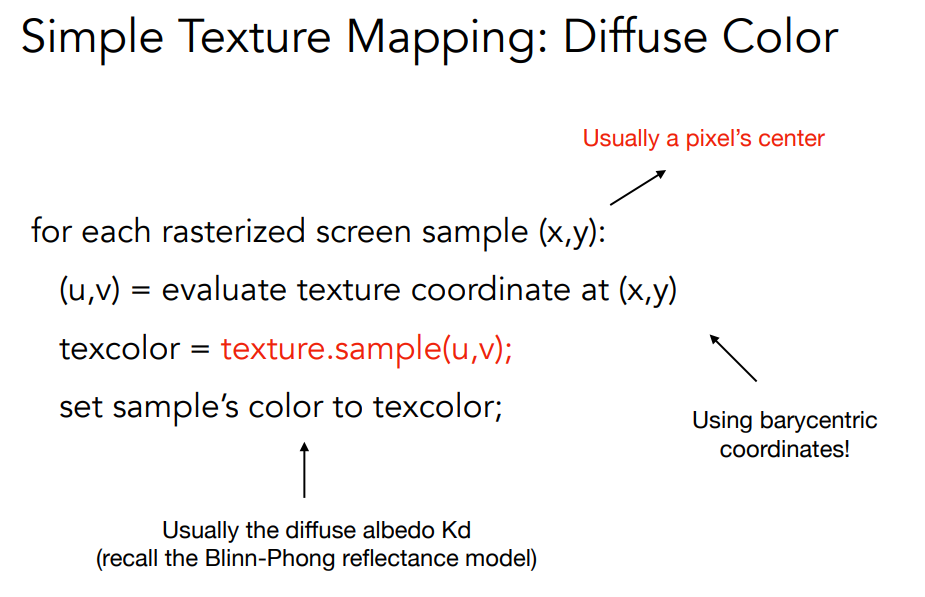
每个vertex rasterize之后坐标与贴图上某个坐标对应

Texture magnification

当纹理图像的分辨率低于显示屏上需要的分辨率时，就会出现纹理放大的情况。例如，当你将一个小纹理贴图拉伸到一个较大的表面上时，就会遇到纹理放大。这个过程需要决定如何在纹理中插值以生成更多的像素

如果texture分辨率太小的解决方法.

放大纹理时常用的插值方法有：

最近邻插值（Nearest Neighbor Interpolation）：这种方法简单高效，但通常会产生锯齿状的边缘，因为它只是选择最接近的纹理像素。
双线性插值（Bilinear Interpolation）：这种方法通过对周围的四个纹理像素进行加权平均，可以生成较为平滑的结果。
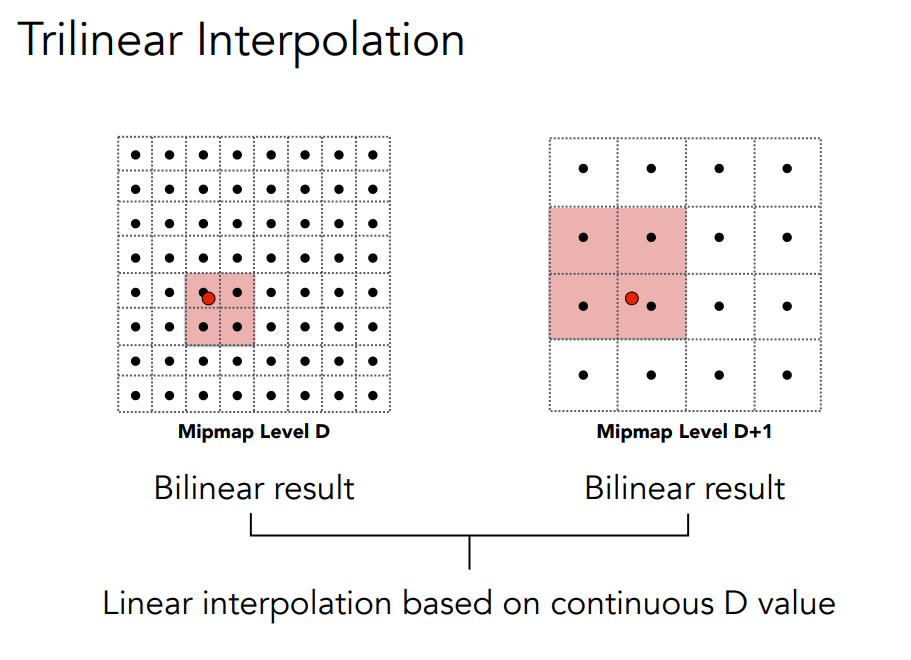
三线性插值（Trilinear Interpolation）：在双线性插值的基础上，加入了对不同MIP贴图层次的线性插值，以进一步提高质量。

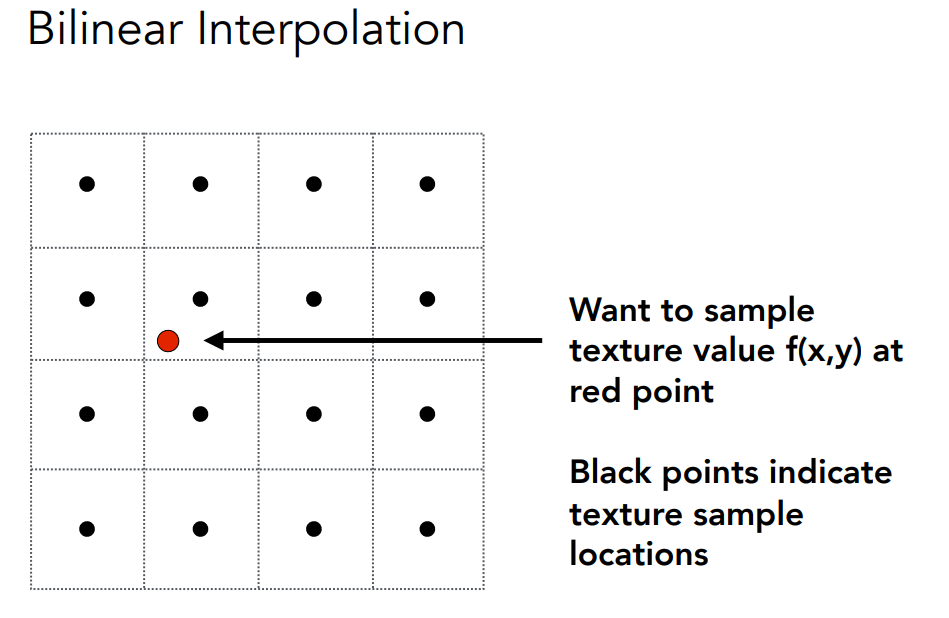
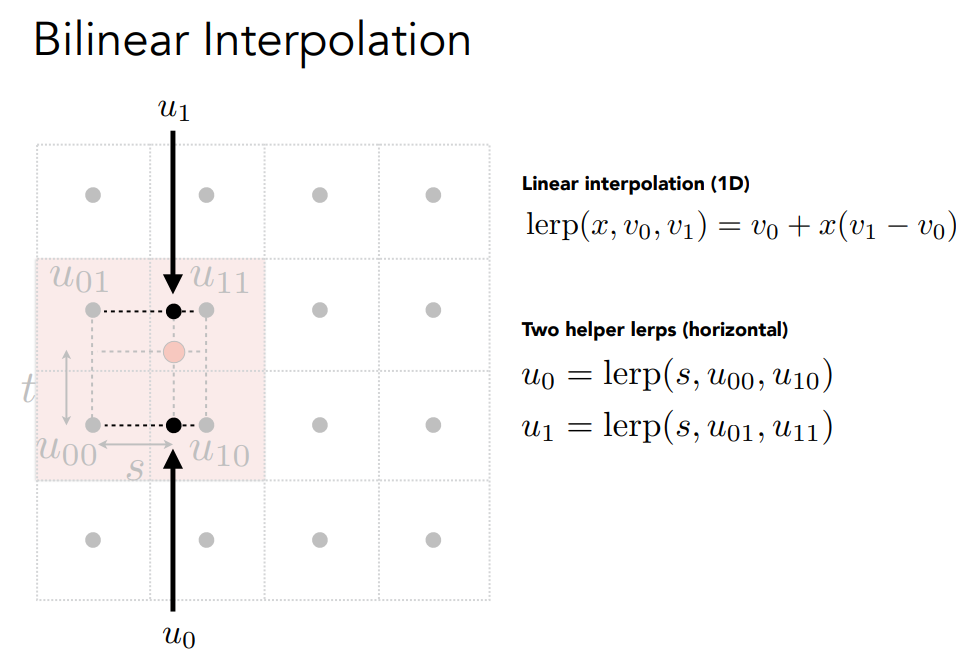
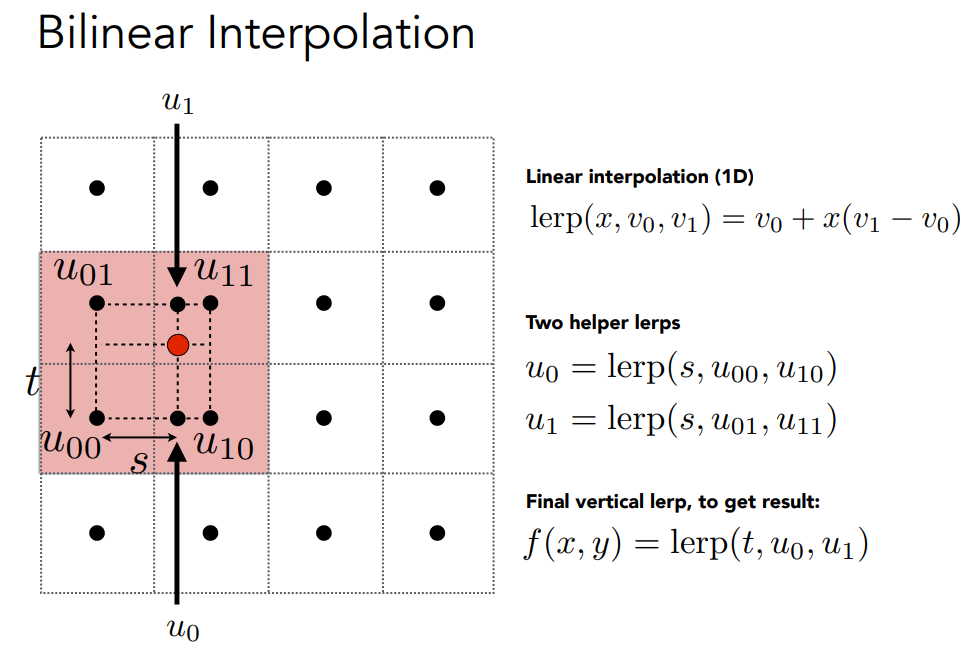
如果texture太大,需要将多个texel取均值分给一个pixel.

Texture minification

纹理缩小发生在纹理图像的分辨率高于显示屏上需要的分辨率时。例如，当你将一个大纹理贴图缩小到一个较小的表面上时，就会遇到纹理缩小。这个过程需要决定如何对纹理进行采样，以避免混叠效应（aliasing）

缩小纹理时常用的方法有：

MIP贴图（Mipmapping）：这是最常用的方法，它预先生成一系列缩小分辨率的纹理图像（MIP层），在渲染时根据需要选择合适的层进行采样，以减少混叠效应。MIP贴图通常与三线性插值结合使用。
各向异性过滤（Anisotropic Filtering）：在MIP贴图的基础上，这种方法进一步提高了纹理在不同角度下的清晰度，特别是在视角较大时效果明显。

Mipmap

mipmap是一种多级纹理映射技术.它通过预先生成并存储一系列逐渐降低分辨率的纹理图像来实现.每个降低分辨率的纹理图像称为一个MIP层

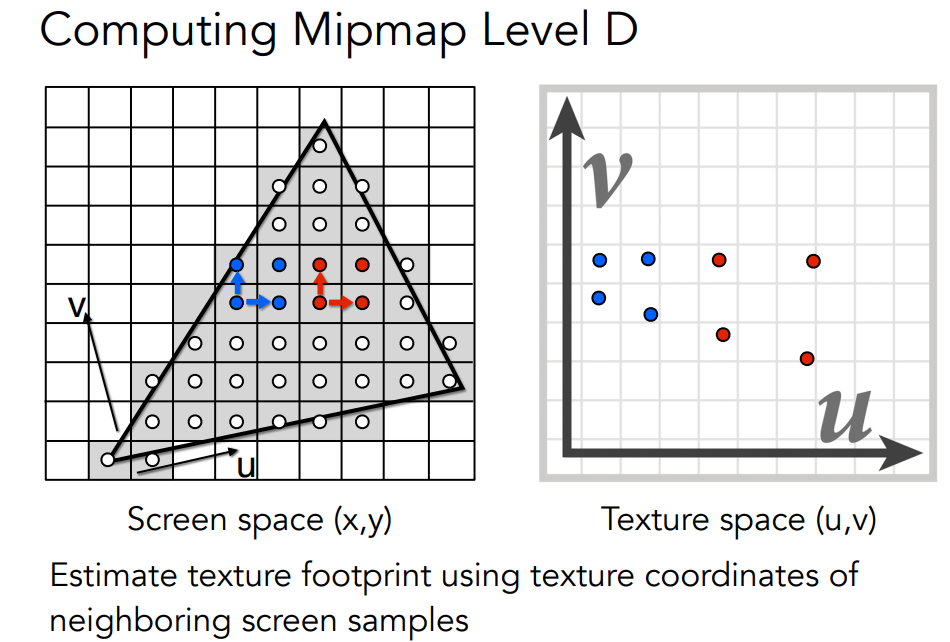
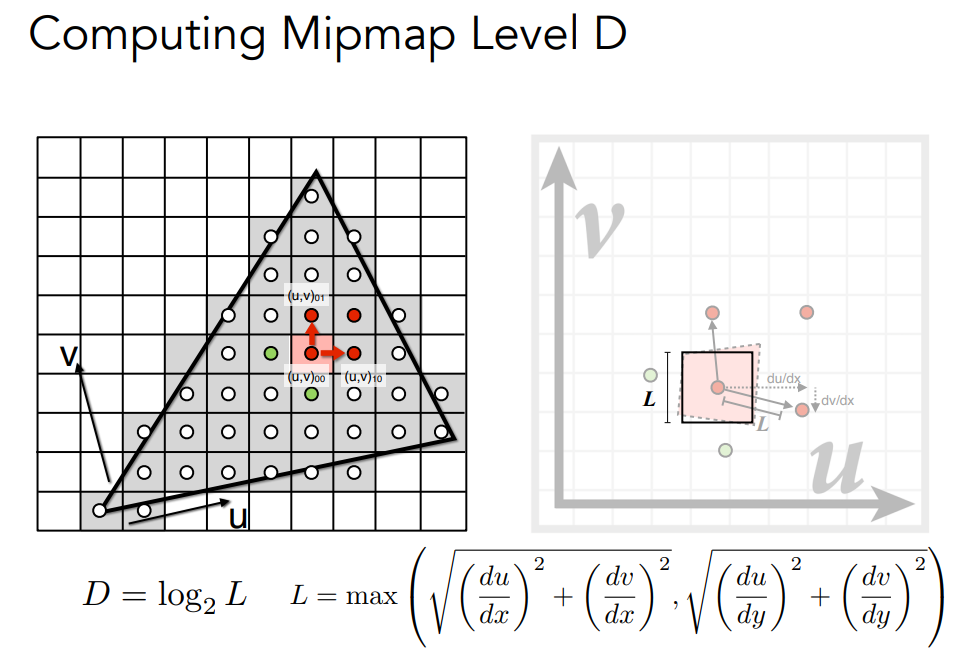
将得到的D四舍五入

在mipmap上再进行插值,

作业要求实现normal_fragment_shader,利用了(法向量+1)/2作为颜色.还有Blinn-Phong反射模型,以及纹理.

normal_fragment_shader比较简单,直接穿法向量即可.

Blinn-Phong反射模型按照公式写即可.

纹理模型主要需要使用对应uv位置的颜色,将原本使用的颜色替换用来算diffuse light.

实现纹理时可以考虑texture magnification的双线性插值,以及minification的mipmap.

Eigen::Vector3f getColorBilinear(float u, float v) {
  auto u_img = u * width;
  auto v_img = (1 - v) * height;
  float v11 = ceil(v_img);
  float v01 = floor(v_img);

  float u01 = floor(u_img);
  float u11 = ceil(u_img);

  auto rightBottomColor = image_data.at<cv::Vec3b>(v01, u11);
  auto leftBottomColor = image_data.at<cv::Vec3b>(v01, u01);
  auto rightTopColor = image_data.at<cv::Vec3b>(v11, u11);
  auto leftTopColor = image_data.at<cv::Vec3b>(v11, u01);
  float s = (u_img - u01) / (u11 - u01);
  float t = (v_img - v01) / (v11 - v01);
  auto topColor = leftTopColor + s * (rightTopColor - leftTopColor);
  auto bottomColor =
      leftBottomColor + s * (rightBottomColor - leftBottomColor);
  auto final_color = bottomColor + t * (topColor - bottomColor);
  return Eigen::Vector3f(final_color[0], final_color[1], final_color[2]);
}

进阶方法包括Bump mapping,有了凹凸效果,还有displacement mapping.

Bump mapping算法

HW4

Geometry 表示几何形状的几种方法,包括显示和隐式.

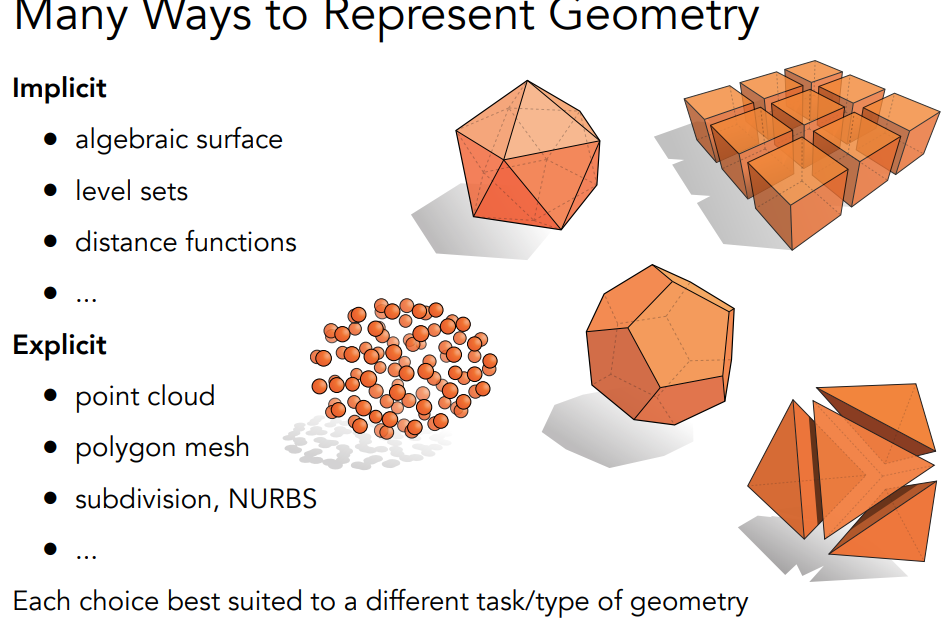
隐式描述优点:

描述简洁（如函数）
便于某些查询（物体内部、与表面的距离）
适用于射线与曲面的交叉（稍后详述）
对于简单形状，可精确描述/无采样误差
易于处理拓扑结构的变化（如流体

缺点

难以模拟复杂形状

显示模型包括点云,多边形网格(polygon mesh),

点云

最简单的表示方法：点列表（x,y,z）
可轻松表示任何几何图形
适用于大型数据集（>>1 点/像素）
通常转换为多边形网格
难以绘制采样不足的区域

多边形网格

存储顶点和多边形（通常为三角形或四边形）
更易于处理/模拟、自适应采样
数据结构更复杂
可能是图形中最常见的表示法

曲线

Bézier Curves

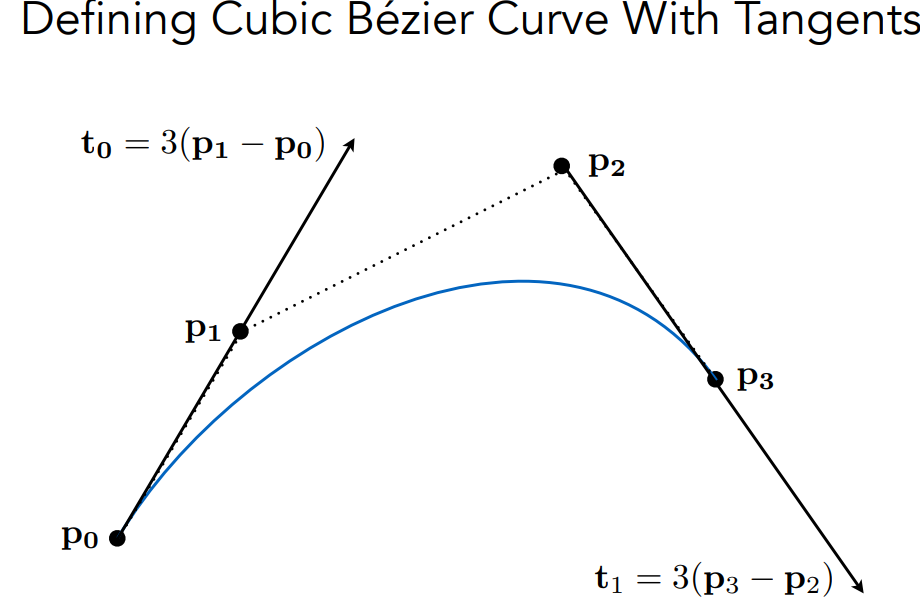
还有cubic贝塞尔曲线,其实就是order更高.

这些曲线都可以归结为多项式.de Casteljau算法

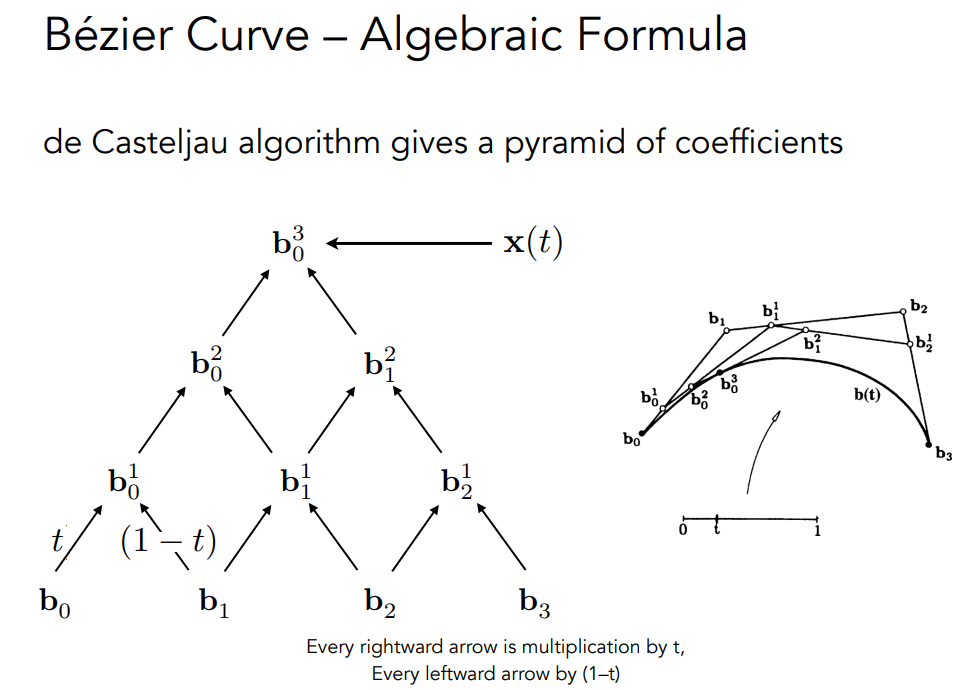
贝塞尔曲线特点

内插端点
与端点相切
仿射变换特性

通过变换控制点来变换曲线
convex hull property
曲线位于控制点的凸边内

利用Piecewise Bézier Curves,将连续的低阶贝塞尔曲线连在一起.

曲线除了贝塞尔曲线,还有splines和B-splines.

Bézier Surfaces

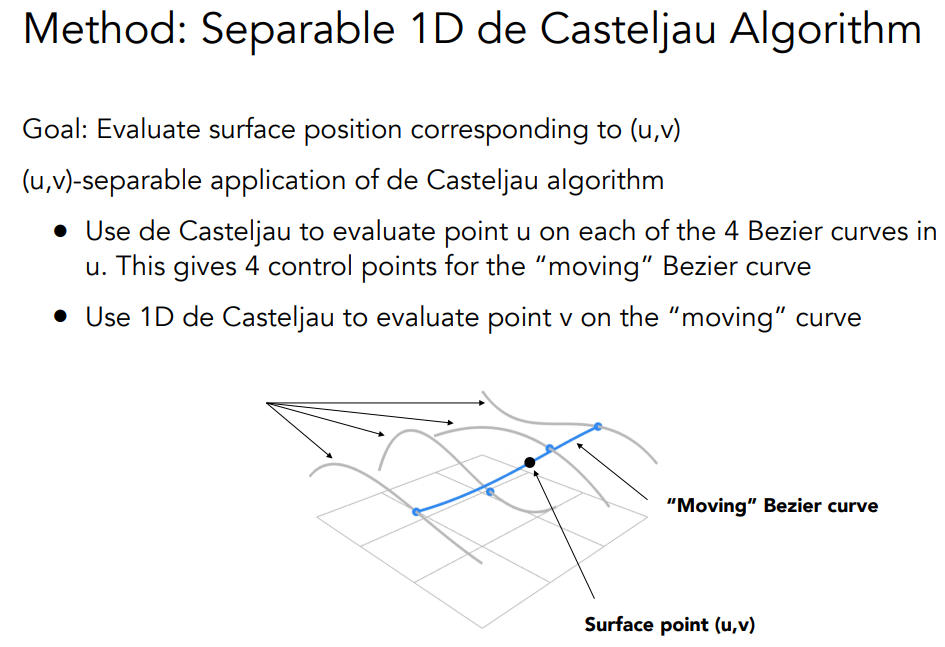
Mesh

对mesh的操作包括subdivision,simplification以及regularization.

subdivision就是将三角形split然后根据一些权重重新分配三角形位置.

此外还有catmull-clark subdivison.

simplification

shadow mapping

不在阴影中的点必须同时被灯光和摄像机看到

作业就是画贝塞尔曲线并反走样.通过[0,1]的t值确定曲线点。naive的方法就是使用多项式直接算,更好的方法是,根据四个点反复的插值得到曲线点. 反走样就是antialiasing,将曲线点的附近点的值赋值,可以根据距离.

cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points,
                             float t) {
  // TODO: Implement de Casteljau's algorithm
  // 首先，将相邻的点连接起来以形成线段
  if (control_points.size() == 1) {
    return control_points[0];
  }
  std::vector<cv::Point2f> points;
  for (int i = 0; i < control_points.size() - 1; i++) {
    auto point = t * control_points[i] + (1 - t) * control_points[i + 1];
    points.push_back(point);
  }
  return recursive_bezier(points, t);
  //  用 t : (1 − t) 的比例细分每个线段，并找到该分割点

  // 得到的分割点作为新的控制点序列，新序列的长度会减少一。
  // 如果序列只包含一个点，则返回该点并终止。否则，使用新的控制点序列并
  // 转到步骤 1。
}

void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) {
  // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de
  // Casteljau's recursive Bezier algorithm.
  float max_dist = 1.5f * sqrt(2);
  for (float t = 0; t <= 1.0f; t += 0.001) {
    auto point = recursive_bezier(control_points, t);
    for (int i = round(point.x) - 1; i < round(point.x) + 2; i++) {
      for (int j = round(point.y) - 1; j < round(point.y) + 2; j++) {
        auto samplePoint = cv::Point2f(i, j);
        float d = cv::norm(samplePoint - point);
        float color = 255.0f * (1 - d / max_dist);
        window.at<cv::Vec3b>(samplePoint.y, samplePoint.x)[2] =
            std::max(window.at<cv::Vec3b>(samplePoint.y, samplePoint.x)[2],
                     (uchar)color);
      }
      // window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }
  }
}

HW5

走过了Rasterization和Geometry,终于到了也令人激动的Ray tracing.

在计算机图形学渲染中,我们通常会模拟Light Rays的传播过程,以计算光照效果。主要方法包括:

光线追踪(Ray Tracing): 从观察者视角发射光线,模拟其在场景中的传播过程。
光栅化(Rasterization): 直接计算每个像素的颜色,不追踪光线的具体传播过程。
辐射度函数(Radiance Function): 利用数学模型描述Light Rays在空间中的传播特性。

光栅化的缺点:不能处理全局的效果,光反射会超过一次.

Ray tracing is accurate, but is very slow

Ray-Tracing的算法

Light Rays

Light Rays的主要特点如下:

传播方向: Light Rays沿直线传播,遵循光线传播的直线性质。
强度衰减: Light Rays的强度随着传播距离的增加而衰减,遵循逆平方定律。
反射和折射: 当Light Rays遇到物体表面时,可能会发生反射或折射,遵循光学定律。

Ray Casting

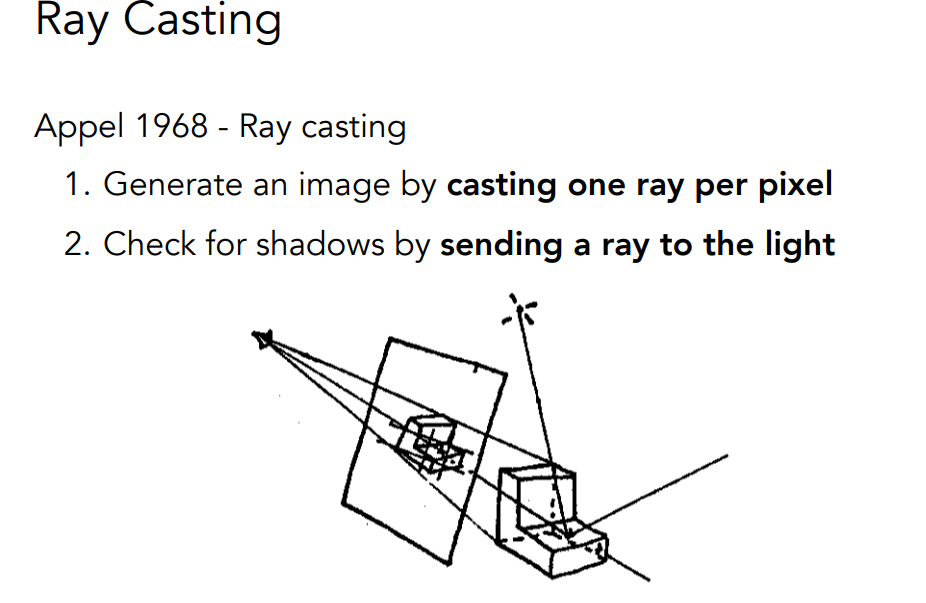
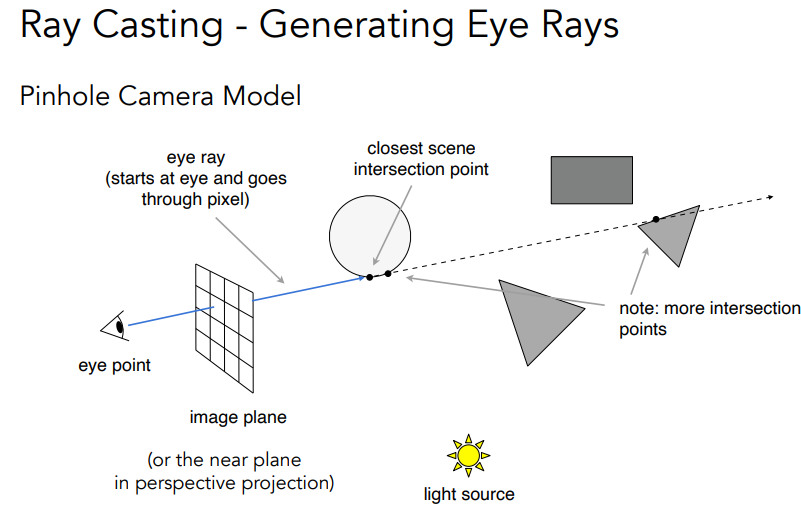
Shadow Rays是光线追踪算法中一个非常重要的技术,它用于计算物体在三维场景中投射出的阴影.

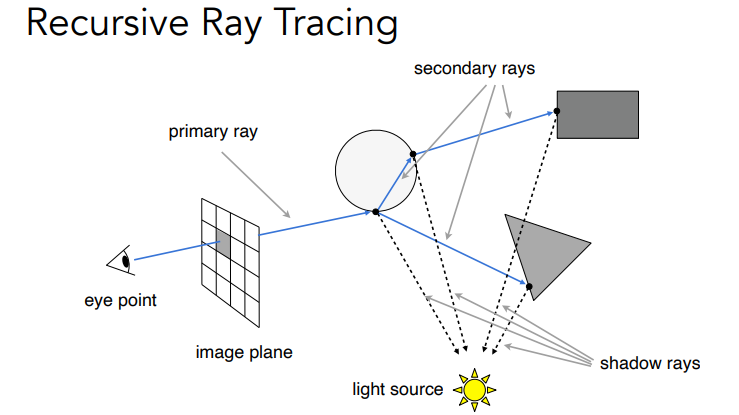
在光线追踪渲染过程中,当一条光线与场景中的物体发生相交时,通常需要判断该点是否位于阴影中。为此,我们会发射一条从交点出发指向光源的shadow ray.

如果这条shadow ray在到达光源之前与任何其他物体相交,那么该交点就位于阴影中.

Ray-Surface Intersection

Ray is defined by its origin and a direction vector

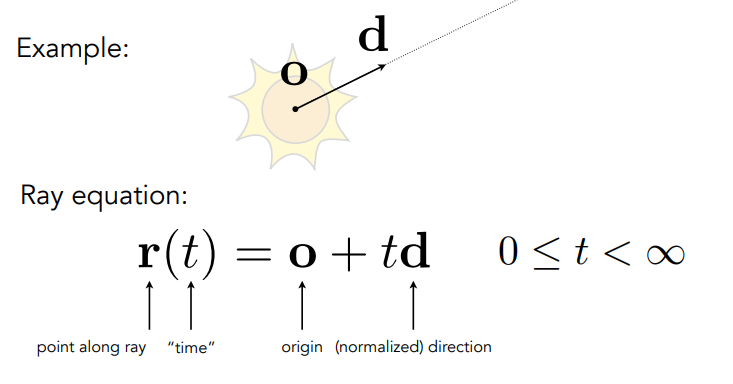
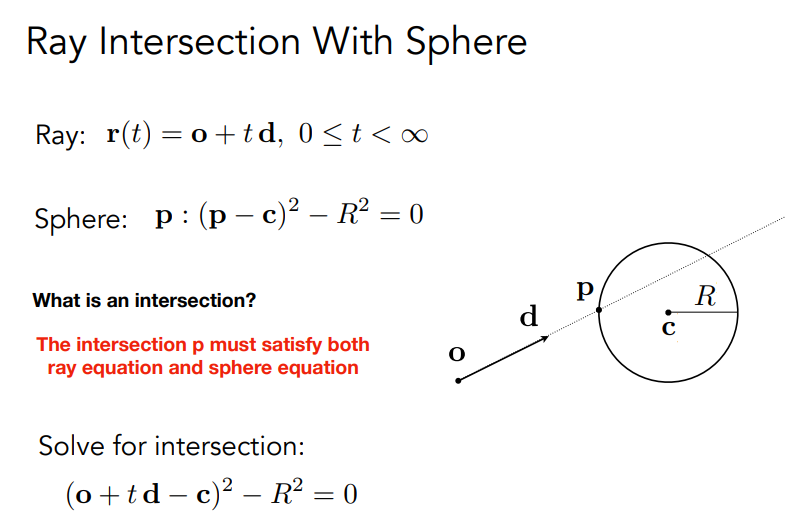
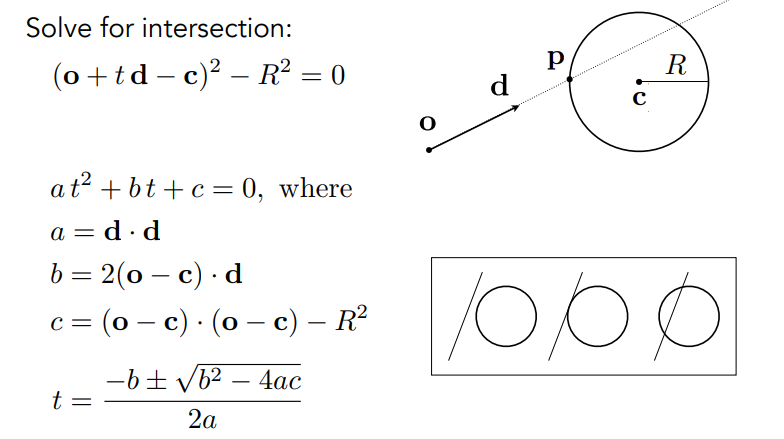
与隐式表示的surface相交的ray计算.

与三角形mesh交叉

简单的想法是让ray与每一个triangle交叉,ray-plane交叉,看点是否在三角形内部.

平面由法向量和面上的一个点定义.

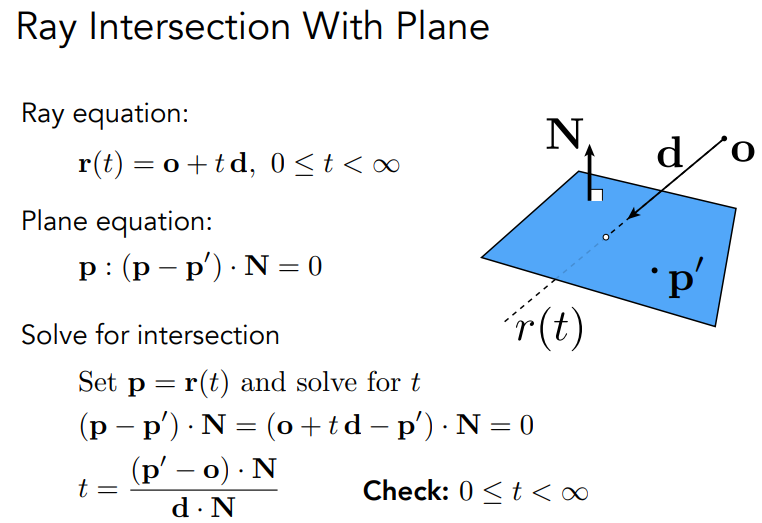
Möller Trumbore Algorithm

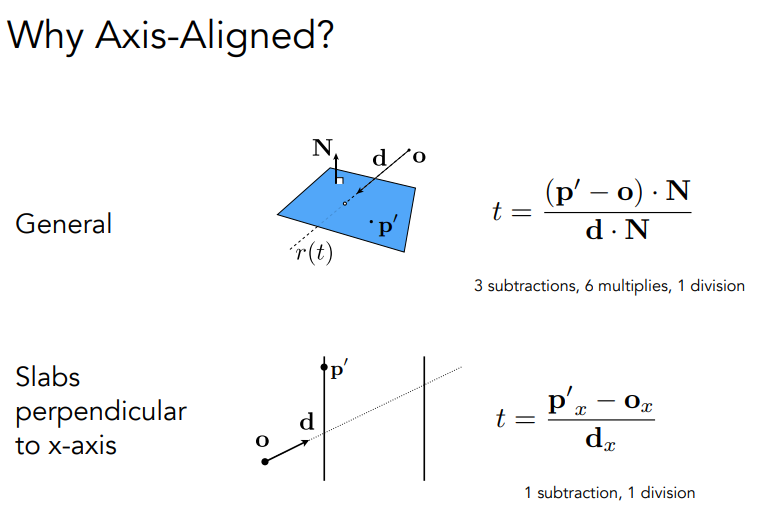
Bounding Volumes

使用这东西来看有没有相交.

box is the intersection of 3 pairs of slabs

这样做的好处

简单的光线-场景交点求解

穷尽地测试每个三角形与光线的交点
找到最近的交点(即最小的t值)

问题:

朴素算法 = #像素 ⨉ # 三角形 (⨉ #反射次数)
非常慢!

快速避免交点的方法:用简单的体积包围复杂物体

物体完全包含在该体积中
如果光线没有击中该体积,就不会击中该物体
所以先测试包围体积,如果击中了,再测试物体本身

Render的方法,其实就是坐标系的一个变换以及castRay算反射以及阴影等.

计算Render的过程:

首先需要使用帧的尺寸来对像素位置进行归一化。
归一化后的像素坐标被称为NDC空间(Normalized Device Coordinates)。
在将像素坐标转换到NDC空间时,我们需要在原始坐标上加上0.5的偏移量。这是为了确保最终的相机光线穿过像素的中心。
NDC空间中的像素坐标范围是[0, 1]。这与光栅化领域中NDC空间的范围[-1, 1]不同。
由于成像平面是以世界坐标系的原点为中心的,因此我们需要进一步将[0, 1]范围的NDC坐标映射到[-1, 1]的范围内。这样做可以确保左侧像素有负的x坐标,右侧像素有正的x坐标,上面的像素有正的y坐标,下面的像素有负的y坐标。
当图像的长宽比不是1:1时,我们需要考虑图像的宽高比。
对于一个7x5像素的图像,宽高比是1.4。
在屏幕空间(NDC空间)中,像素坐标范围仍然是[-1, 1]。但由于横向有更多像素,所以像素会被拉伸变形。
为了让像素保持正方形,我们需要将x坐标乘以图像的宽高比1.4。这样可以将x坐标范围拉伸到[-1.4, 1.4]。
这个操作不会影响y坐标,它仍然在[-1, 1]范围内。

rayTriangleIntersect判断是否相交以及是否在三角形内部,公式如下:

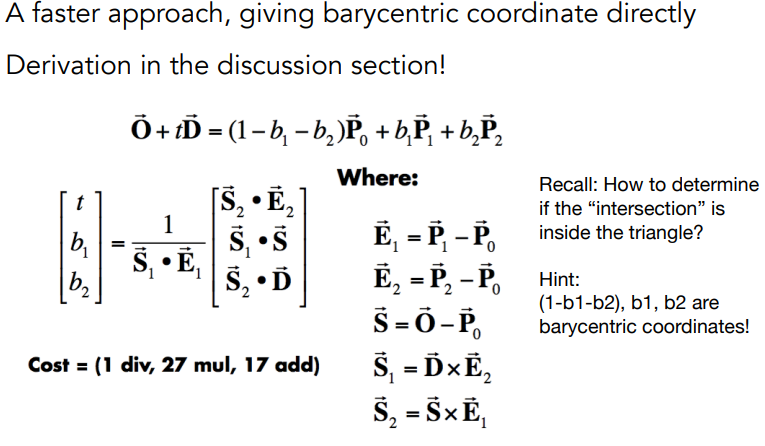
HW6

主要是为了加速ray-tracing的rayTriangle intersection. 进行分割.

包括uniform grid和spatial partitions,前者就是均匀分块,后者包括Oct-Tree,KD-Tree,BSP-Tree多种,还有Bounding Volume Hierarchy的方法.

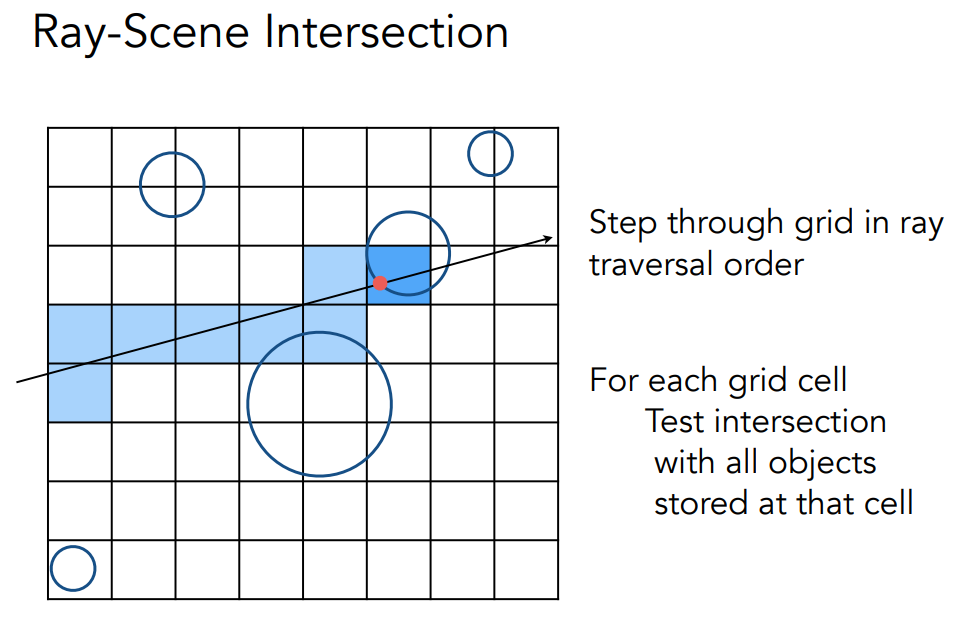
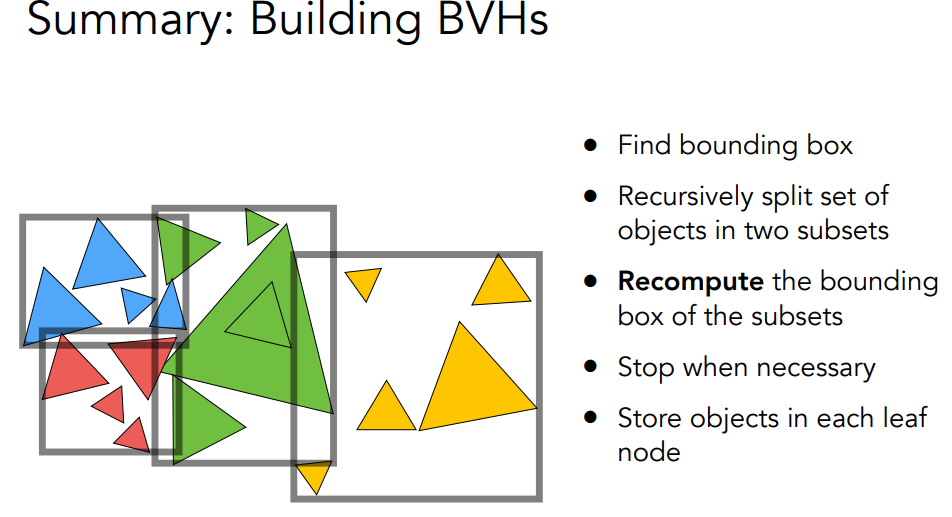
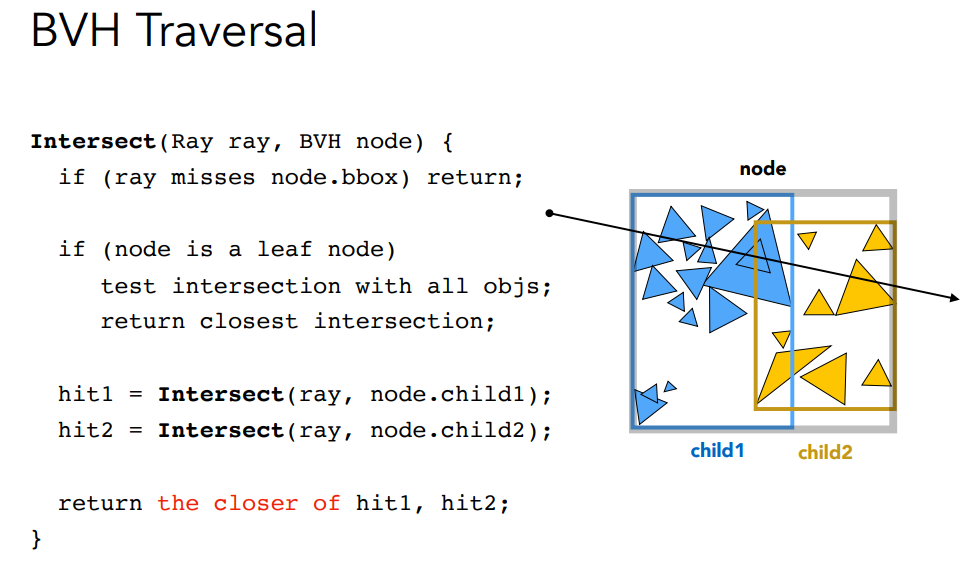
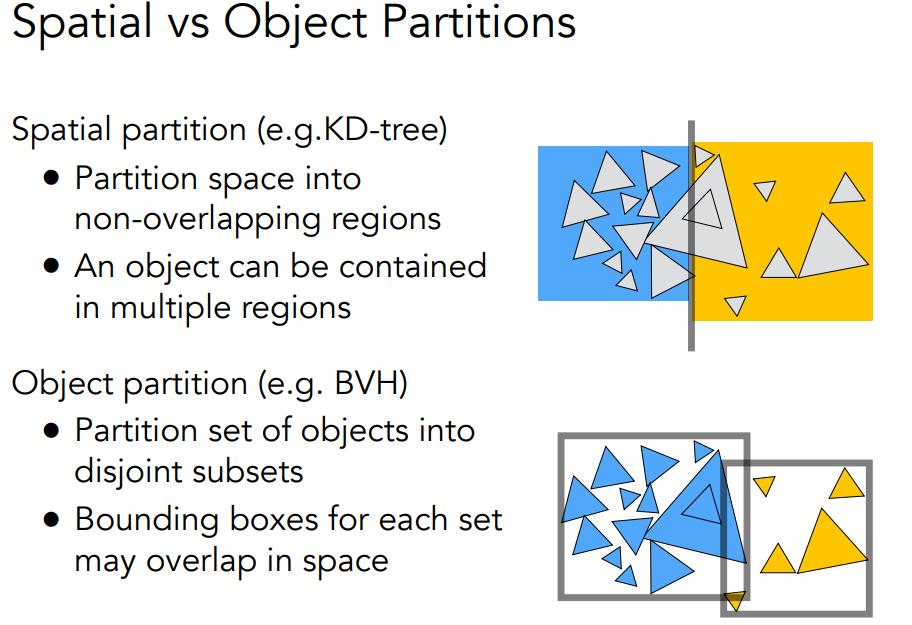
确定ray是否与AABB相交

再确定ray是否与三角形相交,与上一次作业类似.在判断,判断是否与box相交,不相交则没有交点,如果相交,看是否是叶子节点,如果是叶子节点,看是否与其中的object相交,如果不是在分别判断.

Intersection BVHAccel::getIntersection(BVHBuildNode* node,
                                       const Ray& ray) const {
  // TODO Traverse the BVH to find intersection
  Intersection isect;
  if (!node || !node->bounds.IntersectP(ray, ray.direction_inv, {0, 0, 0})) {
    return isect;
  }
  if (node->left == nullptr && node->right == nullptr) {
    return node->object->getIntersection(ray);
  }
  Intersection left = getIntersection(node->left, ray);
  Intersection right = getIntersection(node->right, ray);
  if (left.distance < right.distance) {
    return left;
  } else {
    return right;
  }
  return isect;
}

BVH的构造如下

BVHAccel::BVHAccel(std::vector<Object*> p, int maxPrimsInNode,
                   SplitMethod splitMethod)
    : maxPrimsInNode(std::min(255, maxPrimsInNode)),
      splitMethod(splitMethod),
      primitives(std::move(p)) {
  time_t start, stop;
  time(&start);
  if (primitives.empty()) return;

  root = recursiveBuild(primitives);

  time(&stop);
  double diff = difftime(stop, start);
  int hrs = (int)diff / 3600;
  int mins = ((int)diff / 60) - (hrs * 60);
  int secs = (int)diff - (hrs * 3600) - (mins * 60);

  printf(
      "\rBVH Generation complete: \nTime Taken: %i hrs, %i mins, %i secs\n\n",
      hrs, mins, secs);
}

BVHBuildNode* BVHAccel::recursiveBuild(std::vector<Object*> objects) {
  BVHBuildNode* node = new BVHBuildNode();

  // Compute bounds of all primitives in BVH node
  Bounds3 bounds;
  for (int i = 0; i < objects.size(); ++i)
    bounds = Union(bounds, objects[i]->getBounds());
  if (objects.size() == 1) {
    // Create leaf _BVHBuildNode_
    node->bounds = objects[0]->getBounds();
    node->object = objects[0];
    node->left = nullptr;
    node->right = nullptr;
    return node;
  } else if (objects.size() == 2) {
    node->left = recursiveBuild(std::vector{objects[0]});
    node->right = recursiveBuild(std::vector{objects[1]});

    node->bounds = Union(node->left->bounds, node->right->bounds);
    return node;
  } else {
    Bounds3 centroidBounds;
    for (int i = 0; i < objects.size(); ++i)
      centroidBounds =
          Union(centroidBounds, objects[i]->getBounds().Centroid());
    int dim = centroidBounds.maxExtent();
    switch (dim) {
      case 0:
        std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
          return f1->getBounds().Centroid().x < f2->getBounds().Centroid().x;
        });
        break;
      case 1:
        std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
          return f1->getBounds().Centroid().y < f2->getBounds().Centroid().y;
        });
        break;
      case 2:
        std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
          return f1->getBounds().Centroid().z < f2->getBounds().Centroid().z;
        });
        break;
    }

    auto beginning = objects.begin();
    auto middling = objects.begin() + (objects.size() / 2);
    auto ending = objects.end();

    auto leftshapes = std::vector<Object*>(beginning, middling);
    auto rightshapes = std::vector<Object*>(middling, ending);

    assert(objects.size() == (leftshapes.size() + rightshapes.size()));

    node->left = recursiveBuild(leftshapes);
    node->right = recursiveBuild(rightshapes);

    node->bounds = Union(node->left->bounds, node->right->bounds);
  }

  return node;
}

上面是BVH,再看SAH.

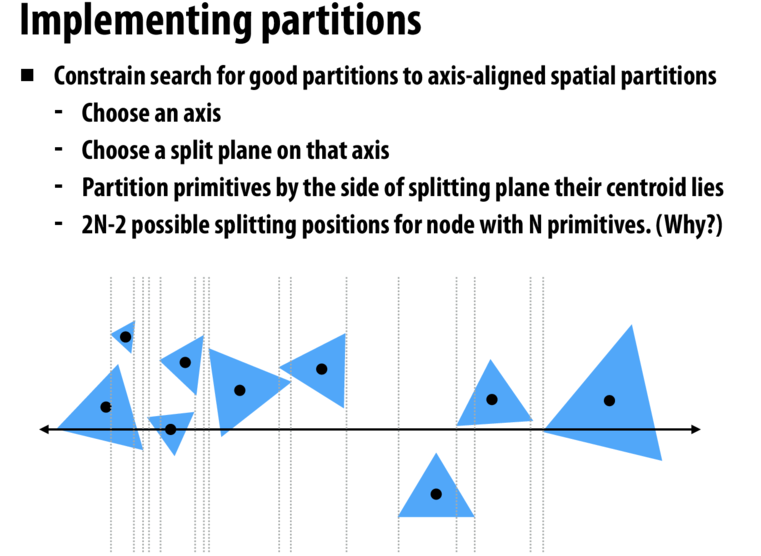
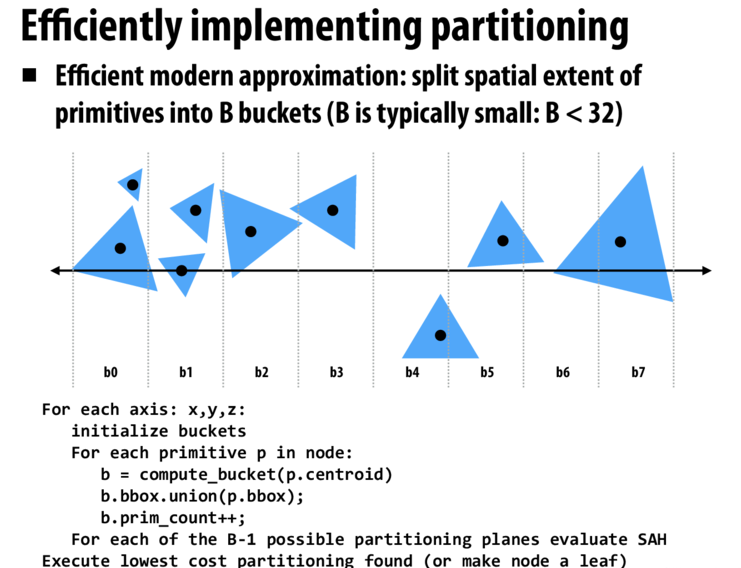
HW7

radiometry

Radiant flux, intensity, irradiance, radiance

辐射能(Radiant energy)是电磁辐射能。它以焦耳为单位

Q [J = Joule]

辐射通量（功率）是单位时间内发射、反射、传输或接收的能量、
单位时间内反射、传输或接收的能量

$\Phi\equiv\frac{\mathrm{d}Q}{\mathrm{d}t}\text{ [W=Watt] [lm=lumen]}$

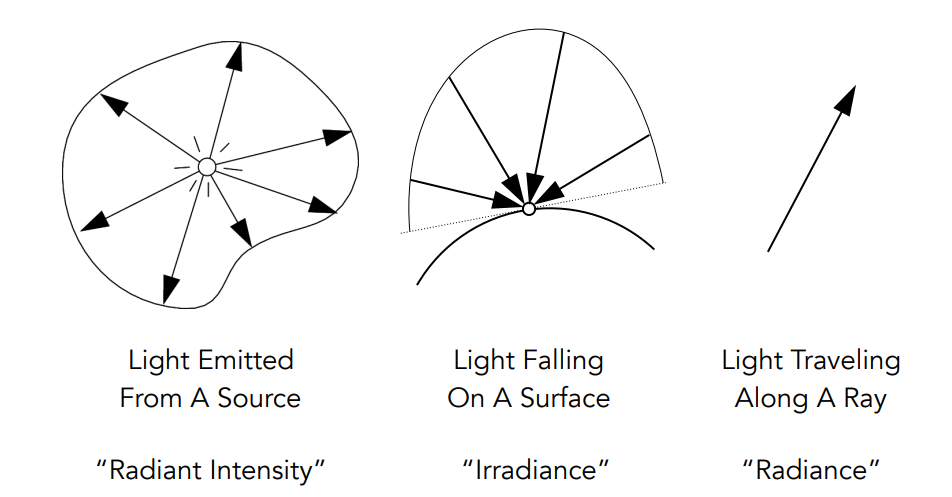
有三个衡量指标,包括intensiry,irradiance和radiance.

实心角：球面上被摄面积与半径平方的比值：球面面积与半径平方之比 ,球有4Π steradians

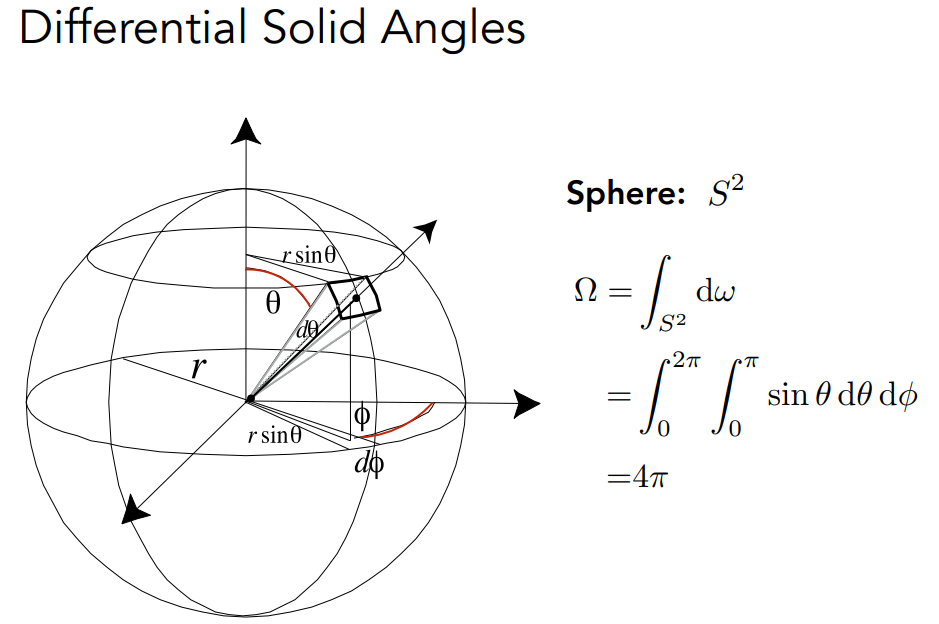
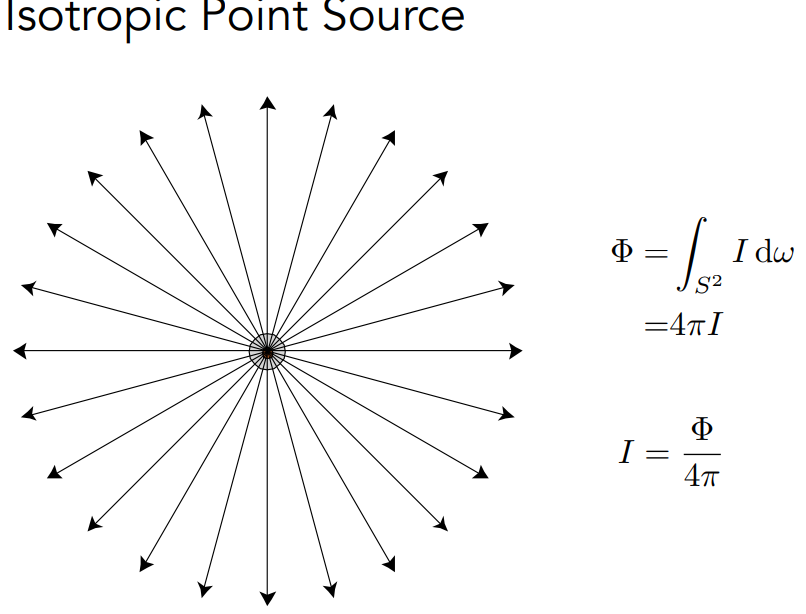
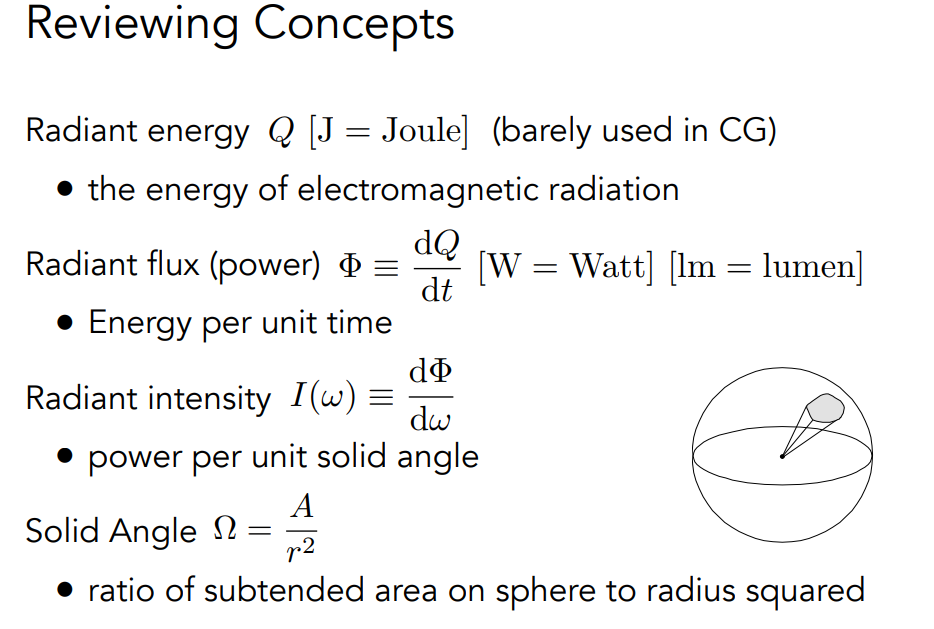
辐照度(irradiance)是入射到表面点的单位面积功率

表面的辐照度与光照方向和表面法线之间夹角的余弦成正比。

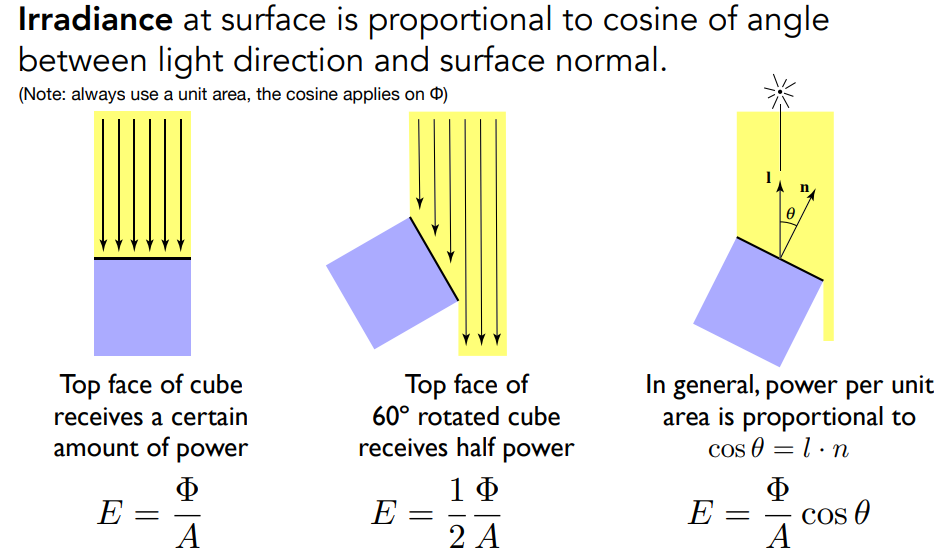
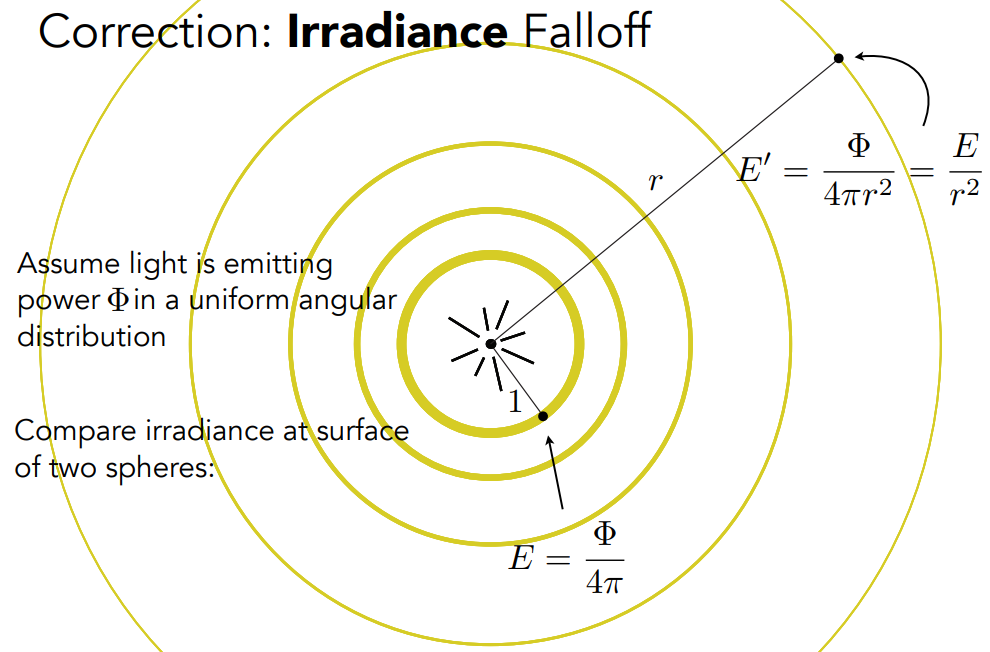
辐射度(Radiance)是描述光在环境中分布的基本场量

辐照度是与光线相关的量
渲染就是计算辐射度

Incident radiance:入射辐射度是到达表面的单位固角辐照度

Exiting Radiance:离开表面辐射度是离开表面的单位投影面积强度。

Bidirectional Reflectance Distribution Function

双向反射分布函数（BRDF）表示从每个入射方向反射到每个出射方向的光量

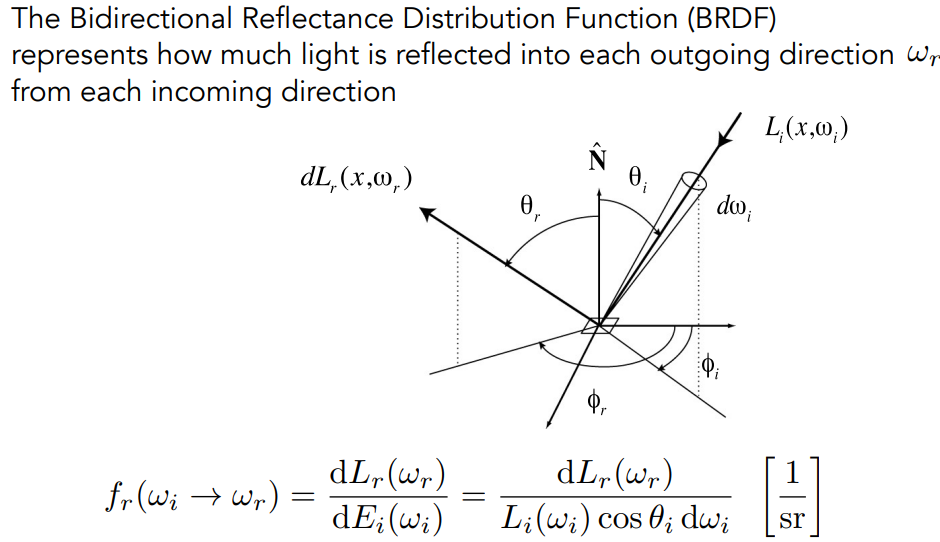
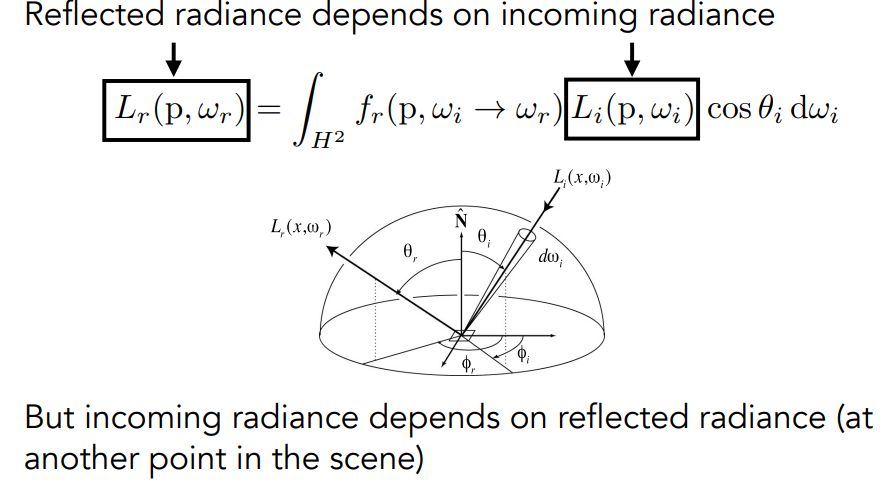
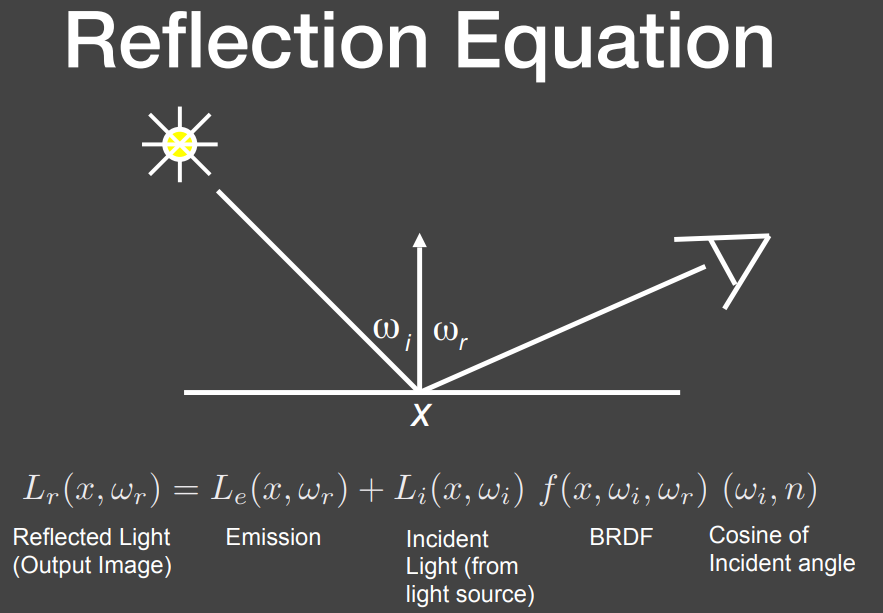
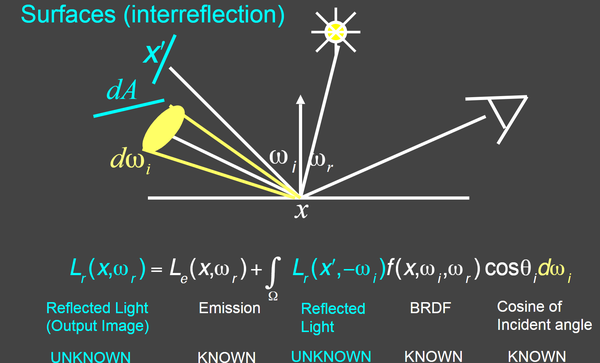
将L~i~转为经过反射后的光L~r~再经过简化.

此时我们令相机接受到的直接光照为：e(u)
最终接收到的光为:l(u)
其他表面弹过来的光为:l(v)
BRDF那些式子为：K（u，v）

Monte Carlo Integration

Path Tracing

光线追踪

始终执行镜面反射/折射
在漫反射表面停止反弹

使用Monte Carlo Integration解决反射公式.

存在的两个问题:

Explosion of #rays as #bounces go up

由于反射,在反射时需要通过蒙特卡洛方法计算多个值,这样多次反射计算量增加.

所以只取一个方向作为入射,但在每个pixel上采样多个值取平均.

The recursive algorithm will never stop

光会无数次反弹. 解决方法:俄罗斯轮盘赌 Russian Roulette (RR)

此外N=1的采样还存在问题:即低采样率的问题，由于我们将平均放到了像素块处用接收到的光线来替代平均着色点的光线，但如果对于一个场景就没有或存在很少的间接光照，主要是直接光照的时候，那这个平均也无法消除误差噪声。

如果光源面积很小，则均匀采样就需要很大的N才能保证采样到光源方向。也就是这里问题来自两个第一个是均匀抽样方法浪费了很多光源不存在的角度

对光采样

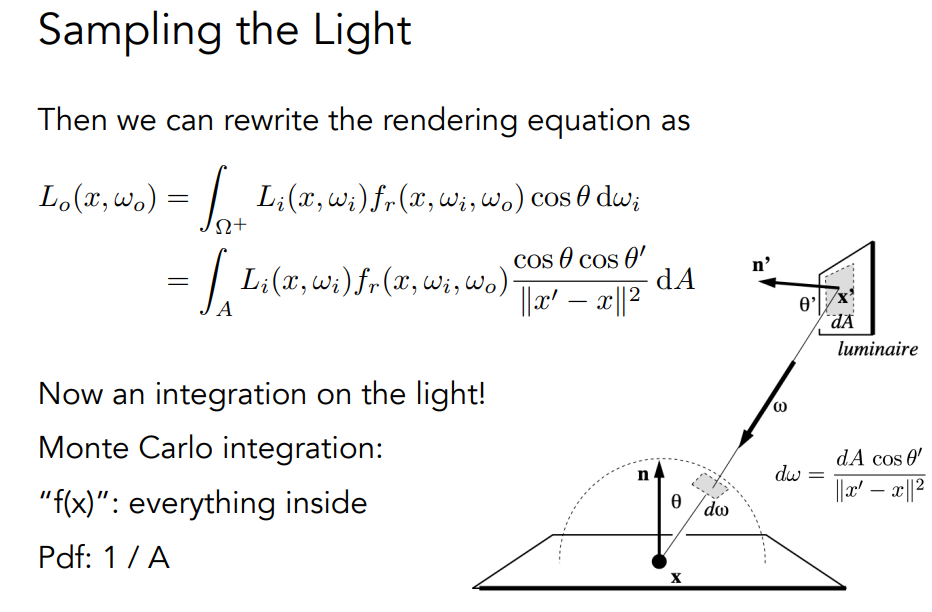
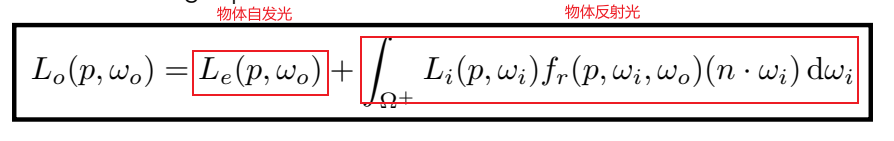
渲染公式通过BRDF得到

演进过程:渲染公式->使用蒙特卡洛方式积分解->引入全局光照,碰到物体会反射->由于反射太多,直接每次只会反射一根光线->由于只反射一根光线,采样不够,在一个pixel上采样更多次->此外这个算法会无穷的进行下去(因为最后只在打到灯光后停止),每次反射通过俄罗斯转盘减少能量->此外还是不够有效,考虑sample the light,sample light本身是dA,需要从dw转到dA->现在选择一个区域作为light source直接照射,另外区域都是间接的

// 总体流程如下：
// 从像素打出射线，检查射线是否命中，命中则继续下一步，反之结束
// 对光源表面进行采样，得到一个采样的交点 Intersection 和光源的 pdf
// 检查光源采样点和像素射线交点，两点之间是否有其他物体遮挡，没有遮挡则可计算直接光
// 计算俄罗斯轮盘赌概率，如果成功进行下一步
// 按照像素射线交点材质的性质，给定像素射线入射方向与交点法向量，用某种分布采样一个出射方向，这里是漫反射
// 有了出射方向和交点，得到新的射线，计算是否有命中
// 如果命中了非光源，计算新射线命中交点给原来像素射线交点带来的间接光
// 最后将直接光和间接光结合，得到最初命中的位置的颜色
// Implementation of Path Tracing
Vector3f Scene::castRay(const Ray &ray, int depth) const {
  // TO DO Implement Path Tracing Algorithm here
  Vector3f l_indir{0.f};
  Vector3f l_dir{0.f};
  Intersection ray_inter = intersect(ray);
  if (!ray_inter.happened) {
    // 没有与任何物体相碰
    return l_dir + l_indir;
  }
  float pdf_light;
  Intersection light_inter;
  sampleLight(light_inter, pdf_light);

  Vector3f N = ray_inter.normal;
  Vector3f x = light_inter.coords;
  Vector3f wo = ray.direction;
  Vector3f p = ray_inter.coords;
  Vector3f ws = (x - p).normalized();
  // shoot a ray from p to x
  Ray ray_light_to_p = Ray(p + EPSILON * N, ws);
  auto rpx_inter = intersect(ray_light_to_p);
  Vector3f NN = rpx_inter.normal;
  Material *m = ray_inter.m;
  // if the ray is not blocked in the middle
  if (rpx_inter.happened && rpx_inter.m->hasEmission()) {
    l_dir = rpx_inter.m->getEmission() * m->eval(wo, ws, N) *
            dotProduct(ws, N) * dotProduct(-ws, NN) / (rpx_inter.distance) /
            pdf_light;
  }

  if (get_random_float() < RussianRoulette) {
    Vector3f wi = (m->sample(wo, N)).normalized();
    Ray rpwi(p, wi);
    auto rpwi_inter = intersect(rpwi);
    if (rpwi_inter.happened && !rpwi_inter.m->hasEmission()) {
      l_indir = castRay(rpwi, depth + 1) * m->eval(wo, wi, N) *
                dotProduct(wi, N) / m->pdf(wo, wi, N) / RussianRoulette;
    }
  }
  return m->getEmission() + l_dir + l_indir; //物体表面的emission和直接从光发射的和反射的
}

from GAMES101笔记 (iewug.github.io)

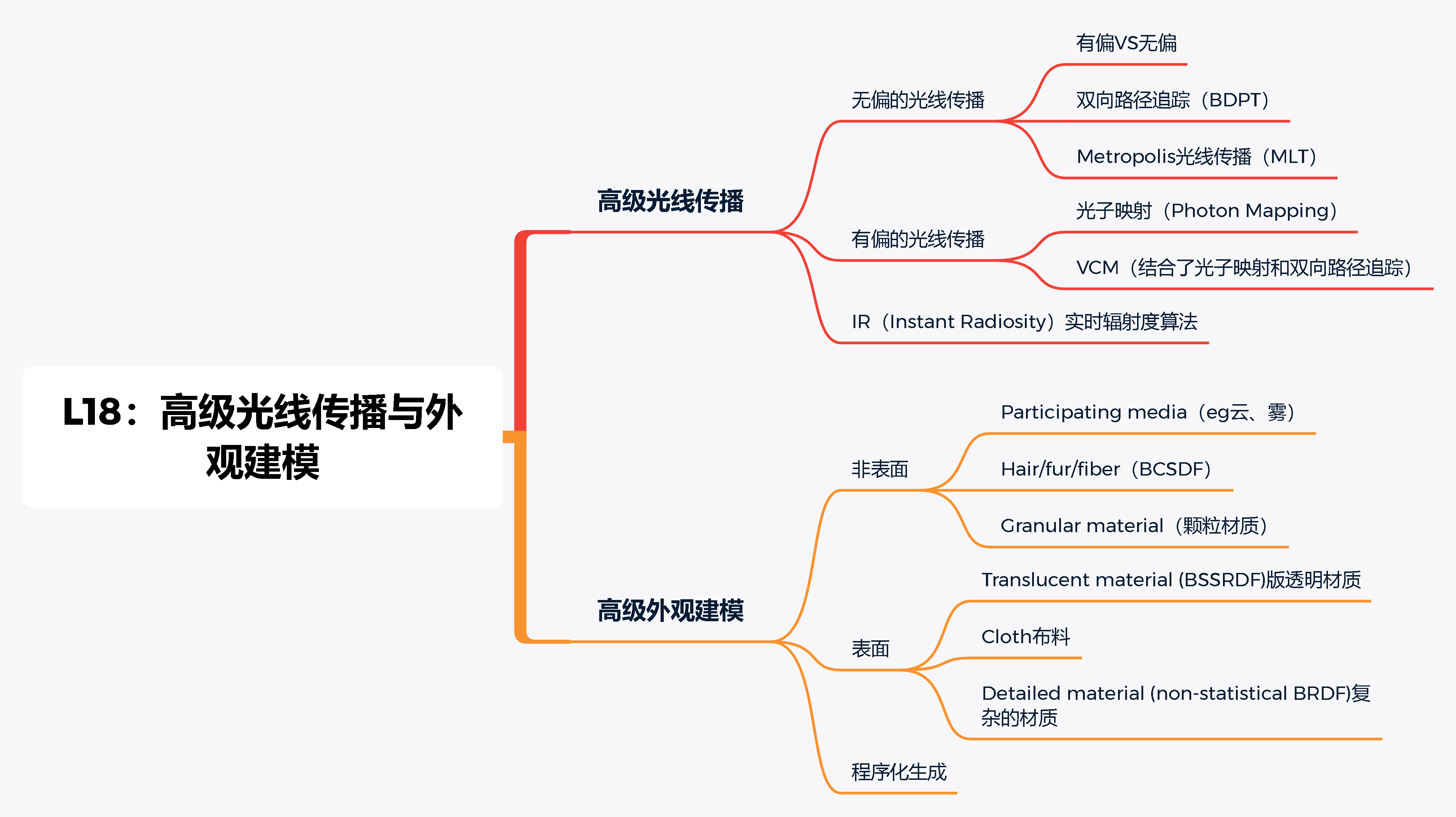
相机与透镜

Shutter Exposes Sensor For Precise Duration

Sensor Accumulates Irradiance During Exposure

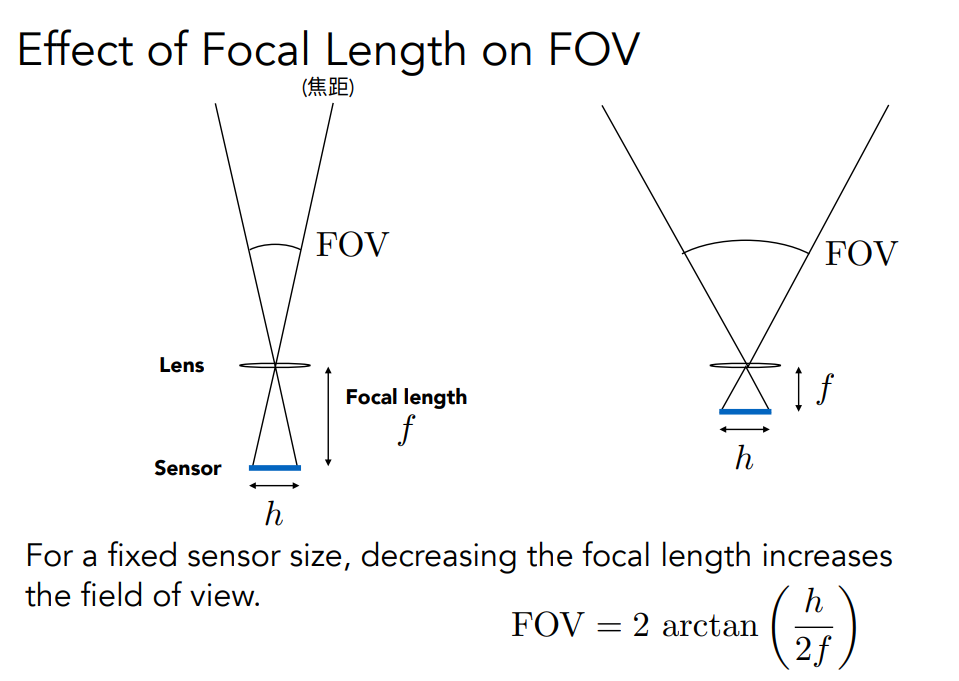
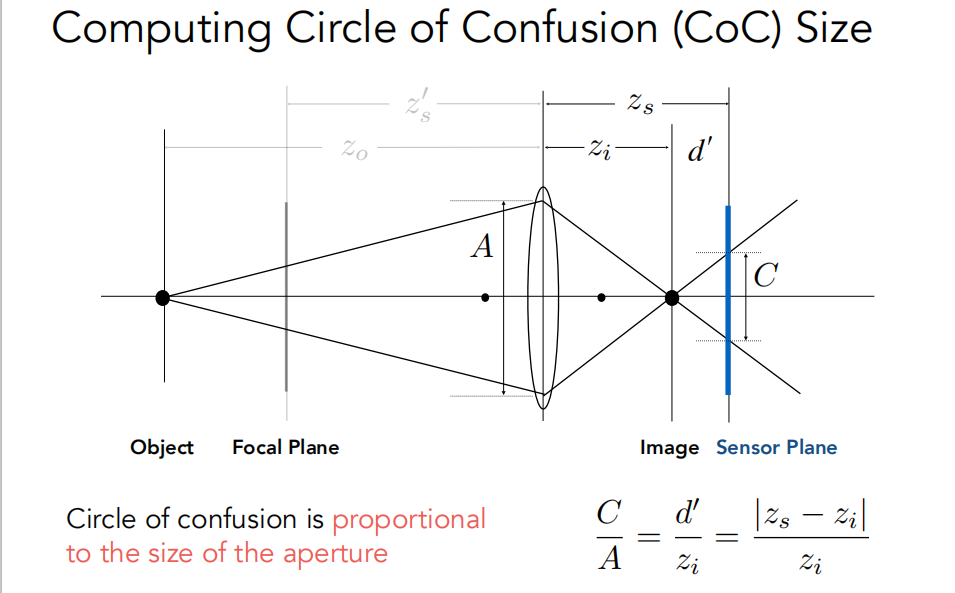
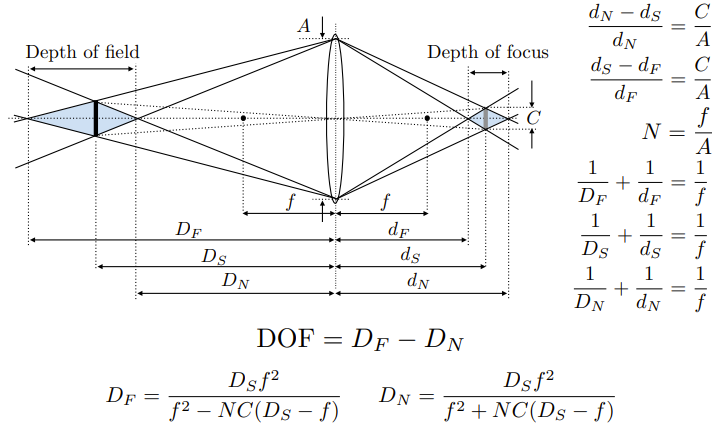
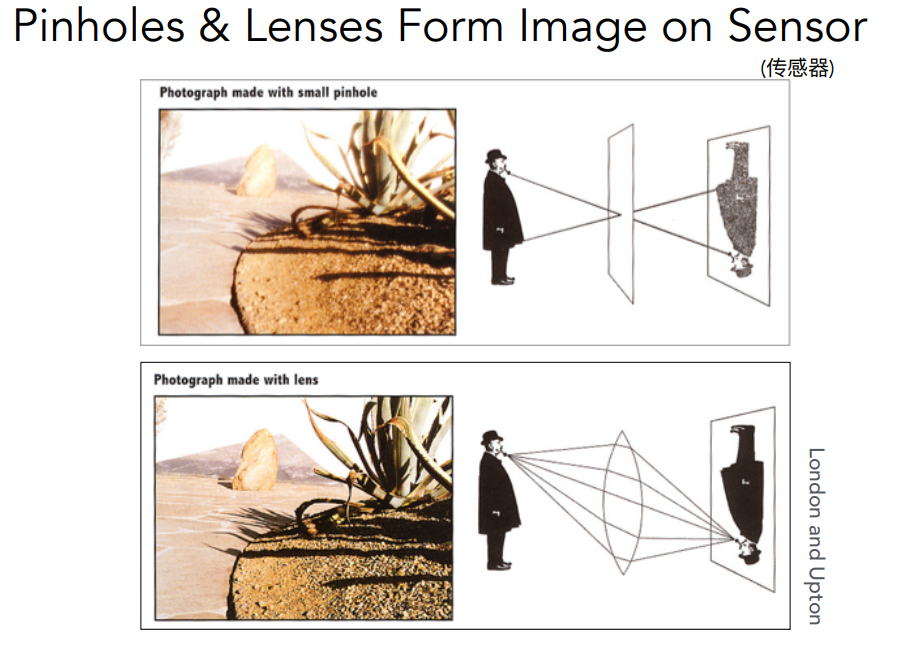
一些概念:focal length,FOV,exposure,ISO(感光度),F-step(焦距除以口径的直径),CoC大小(当物体远离Focal Plane，原本的一个点落在sensor plane上就会变成一个圆),景深,指的是在相机拍摄过程中,成像清晰的范围或深度。

光场、颜色与感知

光场（light field或称为lumigraph），即是空间中任意点发出的任意方向的光的集合

HW8

Mass Spring System 质量-弹簧系统

粒子系统

将动态系统建模为大量粒子的集合
大量粒子的集合,每个粒子的运动由一组
物理（或非物理）力
图形和游戏中的流行技术

易于理解和实施
可扩展：粒子数量越少速度越快，粒子数量越多
以提高复杂性
挑战
可能需要很多粒子（如流体）
可能需要加速结构（如
找到最近的粒子进行交互）

吸引力和斥力

重力、电磁力、…
弹簧、推进力 …
阻尼力
摩擦力、空气阻力、粘滞力 …
碰撞
墙壁、容器、固定物体、 …
动态物体、角色身体部位
正向运动学（forward kinematics）：已知初始的关键点位置和相对旋转，计算最终的关键点位置。唯一解
反向运动学（inverse kinematics）：根据初始的关键点位置和最终关键点位置，计算相对旋转的数学过程。无解或无穷多解（ill-posed problem）。

Rigging(绑定)

装配是对角色进行更高级别的控制，可以更快、更直观地修改角色的姿势、变形和表情等。
更快、更直观地修改姿势、变形和表情等。

就像木偶上的线
捕捉所有有意义的角色的变化
因角色而异
角色制作成本高
手工制作
需要艺术和技术培训

代替骨架，直接在曲面之间插值
例如，建立面部表情集合模型
表情模型：
最简单的方案：对顶点位置进行线性组合
使用样条曲线控制随时间变化的权重选择

Motion Capture(动捕)

创建动画序列的数据驱动方法

记录真实世界中的表演（例如，人在执行一项活动）
从收集到的数据中提取姿势与时间的函数关系

Single Particle Simulation

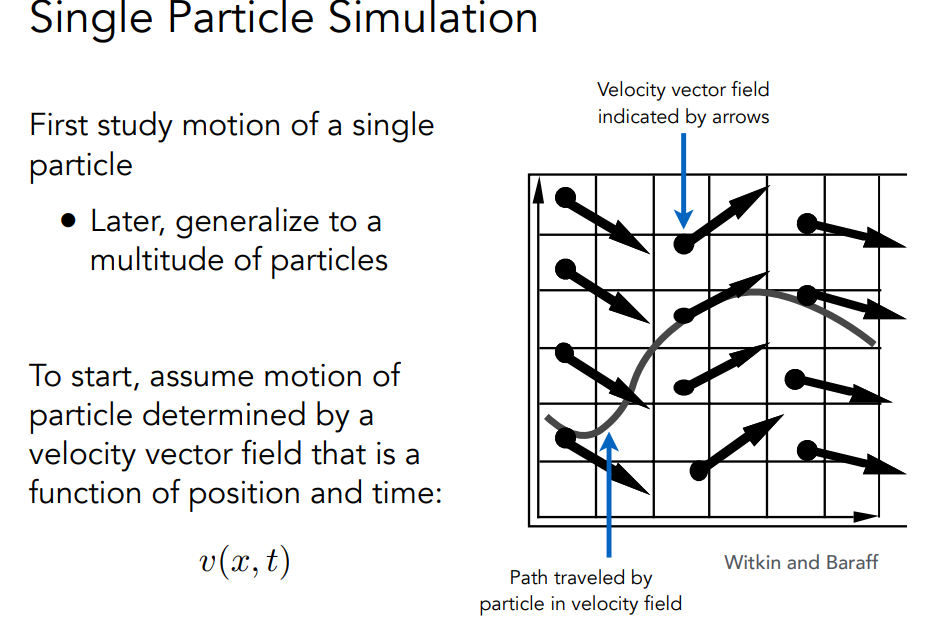首先，假设粒子的运动由速度矢量场决定，速度矢量场是位置和时间的函数：v(x, t)计算粒子随时间变化的位置需要求解一个一阶常微分方程： “一阶 “指的是导数。”普通 “意味着没有 “偏” 导数,即x只是t的函数.

在给定粒子初始位置 x0 的条件下，我们可以通过正向数值积分来求解 ODE

欧拉法（又称前向欧拉法、显式欧拉法）

简单迭代法
常用
非常不准确
经常不稳定

消除不稳定因素

中点法/修正欧拉法

起点和终点的平均速度
自适应步长
递归比较一步和两个半步，直到
误差可接受
隐式方法
使用下一时间步的速度（困难）
基于位置/Verlet 积分
在时间步后约束粒子的位置和速度步

Rope::Rope(Vector2D start, Vector2D end, int num_nodes, float node_mass,
           float k, vector<int> pinned_nodes) {
  // TODO (Part 1): Create a rope starting at `start`, ending at `end`, and
  // containing `num_nodes` nodes.
  for (int i = 0; i < num_nodes; i++) {
    Vector2D pos =
        start + (end - start) * ((double)i / ((double)num_nodes - 1.0));
    masses.push_back(new Mass(pos, node_mass, false));
  }
  for (int i = 0; i < num_nodes - 1; i++) {
    springs.push_back(new Spring(masses[i], masses[i + 1], k));
  }
  for (auto &i : pinned_nodes) {
    masses[i]->pinned = true;
  }

  //        for (auto &i : pinned_nodes) {
  //            masses[i]->pinned = true;
  //        }
}

void Rope::simulateEuler(float delta_t, Vector2D gravity) {
  for (auto &s : springs) {
    // （solving constraints)
    auto mod_ab = (s->m1->position - s->m2->position).norm();
    s->m1->forces += -s->k * (s->m1->position - s->m2->position) / mod_ab *
                     (mod_ab - s->rest_length);
    s->m2->forces += -s->k * (s->m2->position - s->m1->position) / mod_ab *
                     (mod_ab - s->rest_length);
  }

  for (auto &m : masses) {
    if (!m->pinned) {
      auto a = m->forces / m->mass + gravity;
      m->position += m->velocity * delta_t;  //  explicit
      m->velocity += a * delta_t;
      m->position += m->velocity * delta_t;  //  implicit
    }

    // Reset all forces on each mass
    m->forces = Vector2D(0, 0);
  }
}
void Rope::simulateVerlet(float delta_t, Vector2D gravity) {
  for (auto &s : springs) {
    // TODO (Part 3): Simulate one timestep of the rope using explicit Verlet
    // （solving constraints)
    auto mod_ab = (s->m1->position - s->m2->position).norm();
    s->m1->forces += -s->k * (s->m1->position - s->m2->position) / mod_ab *
                     (mod_ab - s->rest_length);
    s->m2->forces += -s->k * (s->m2->position - s->m1->position) / mod_ab *
                     (mod_ab - s->rest_length);
  }

  for (auto &m : masses) {
    if (!m->pinned) {
      Vector2D temp_position = m->position;
      // TODO (Part 3.1): Set the new position of the rope mass
      auto a = m->forces / m->mass + gravity;
      // TODO (Part 4): Add global Verlet damping
      m->position = temp_position + (temp_position - m->last_position) +
                    a * delta_t * delta_t;
      m->last_position = temp_position;
    }

    // Reset all forces on each mass
    m->forces = Vector2D(0, 0);
  }
}
void Rope::simulateVerlet(float delta_t, Vector2D gravity) {
  for (auto &s : springs) {
    // TODO (Part 3): Simulate one timestep of the rope using explicit Verlet
    // （solving constraints)
    auto mod_ab = (s->m1->position - s->m2->position).norm();
    s->m1->forces += -s->k * (s->m1->position - s->m2->position) / mod_ab *
                     (mod_ab - s->rest_length);
    s->m2->forces += -s->k * (s->m2->position - s->m1->position) / mod_ab *
                     (mod_ab - s->rest_length);
  }

  float damping_factor = 0.00005;
  for (auto &m : masses) {
    if (!m->pinned) {
      Vector2D temp_position = m->position;
      // TODO (Part 3.1): Set the new position of the rope mass
      auto a = m->forces / m->mass + gravity;
      // TODO (Part 4): Add global Verlet damping
      m->position = temp_position +
                    (1 - damping_factor) * (temp_position - m->last_position) +
                    a * delta_t * delta_t;
      m->last_position = temp_position;
    }

    // Reset all forces on each mass
    m->forces = Vector2D(0, 0);
  }
}

名词解释

缓冲对象

比如顶点缓冲对象,顶点数组对象.

定义顶点数据以后，我们会把它作为输入发送给图形渲染管线的第一个处理阶段：顶点着色器。它会在GPU上创建内存用于储存我们的顶点数据，还要配置OpenGL如何解释这些内存，并且指定其如何发送给显卡。顶点着色器接着会处理我们在内存中指定数量的顶点。

通过顶点缓冲对象(Vertex Buffer Objects, VBO)管理这个内存，它会在GPU内存（通常被称为显存）中储存大量顶点。使用这些缓冲对象的好处是我们可以一次性的发送一大批数据到显卡上，而不是每个顶点发送一次。从CPU把数据发送到显卡相对较慢，所以只要可能我们都要尝试尽量一次性发送尽可能多的数据。当数据发送至显卡的内存中后，顶点着色器几乎能立即访问顶点，这是个非常快的过程。

缓冲对象类型

比如顶点缓冲对象类型,创建好的缓冲可以绑定到某种对象类型上.

1
2
3

unsigned int VBO;
glGenBuffers(1, &VBO);
glBindBuffer(GL_ARRAY_BUFFER, VBO);

从这一刻起，我们使用的任何（在GL_ARRAY_BUFFER目标上的）缓冲调用都会用来配置当前绑定的缓冲(VBO)。然后我们可以调用glBufferData函数，它会把之前定义的顶点数据复制到缓冲的显存中

1	glBufferData(GL_ARRAY_BUFFER, sizeof(vertices), vertices, GL_STATIC_DRAW);

shader与GLSL

包括顶点着色器等等

VAO

顶点数组对象(又称 VAO)可以像顶点缓冲区对象一样绑定,此后的顶点属性调用都将存储在 VAO 中.

书籍和网站推荐

解题参考

Games101现代计算机图形学入门 - 作业1~8 集合含提高项总结 - lawliet9 - 博客园 (cnblogs.com)

书籍

Fundamentals of Computer GraphicsFCG-Translators/FundamentalsOfComputerGraphics-CN: 计算机图形学基础（中文译本） (github.com)
OpenGL超级宝典（第7版） (豆瓣) (douban.com)

网站