Sekyoro的博客小屋

vqvae及其变体代码学习

发表于 更新于
本文字数： 8.2k 阅读时长 ≈ 7 分钟

vqvae出自[1711.00937] Neural Discrete Representation Learning,用于无监督学习离散表征,目前在多模态生成领域还有使用. 这里学习一下代码

VQVAE

vqvae道理本身很简单,它的提出与pixelcnn、自回归模型息息相关,像vae,gan这种生成式模型,它们更像是对整个数据进行估计,而自回归模型又与序列模型相关,更像是对数据生成分布的建模

自回归模型以序列中的先前值为条件进行预测，而不是基于潜在随机变量。因此，他们试图对数据生成分布进行显式建模，而不是对其进行近似

poixelcnn就是一个自回归模型,而其每次就是从vqvae得到的离散结果中进行采样序列性地生成结果,为了实现这种效果利用了一种masked convolution,将卷积权重后面部分置0,使得在卷积的时候不关注后面的结果ToyPixelCNN.ipynb at master · pilipolio/learn-pytorch

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class MaskedConv(nn.Conv2d):
	def __init__(self, mask_type, *args, **kwargs):
		super(MaskedConv, self).__init__(*args, **kwargs)
		self.mask_type = mask_type
		self.register_buffer('mask', self.weight.data.clone())

		channels, depth, height, width = self.weight.size()

		self.mask.fill_(1)
		if mask_type =='A':
			self.mask[:,:,height//2,width//2:] = 0
			self.mask[:,:,height//2+1:,:] = 0
		else: 
			self.mask[:,:,height//2,width//2+1:] = 0
			self.mask[:,:,height//2+1:,:] = 0


	def forward(self, x):
		self.weight.data *= self.mask 
		return super(MaskedConv, self).forward(x)

现在许多的模型,包括transformer都是auto-regressive的,而GAN与VAE并不是,它们的缺点就是难以建模离散数据.而vqvae就弥补了这一点.

而VQVAE中重点其实是设计好一个离散字典后,使用了一种技巧将梯度传导使得能够更新这个字典.

这种设计称作直通估计器,将decoder得到的梯度直接传到了encoder.假设codebook的shape是[codebook_size,codebook_dim],输入特征shape是[size,codebook_dim],通过一个指标得到它们的距离(可以使用torch.cdist)得到[size,codebook_size],这相当于得到了特征上每个位置在字典上对应的位置.

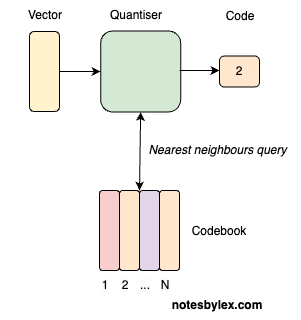
Vector Quantisation

1
2
3
4
5
6
7
8
9
10
# 写法1
dist_manual = torch.sqrt(
        torch.sum(x ** 2, dim=1, keepdim=True) +
        torch.sum(y ** 2, dim=1, keepdim=True).t() -
        2 * x @ y.t()
    )
# 写法2 better readable and efficient since no gradient computation
      with torch.no_grad():
            dist = torch.cdist(x, implicit_codebook)
            indices = dist.argmin(dim = -1)

根据最近的距离得到嵌入后的特征

1
2
3
4
5
6
7
8
# 写法1  
min_encoding_indices = torch.argmin(d, dim=1).unsqueeze(1)  # (encoded_feat size,1)
        min_encodings = torch.zeros(
            min_encoding_indices.shape[0], self.n_e, device=z.device)  # (encoded_feat size,embedding_size)
        min_encodings.scatter_(1, min_encoding_indices, 1)  # one-hot  like
# 写法2 dry and more clean
min_encoding_indices = torch.argmin(d, dim=1)
    my_min_encodings = F.one_hot(min_encoding_indices.squeeze())

one-hot的shape是[encode_size,embed_size],下面公式中第三项是commitment loss,用于更新encoder输出,第三项用于更新字典

为了学习嵌入空间，使用最简单的字典学习算法之一，向量量化( VQ )。VQ目标使用l2误差将嵌入向量ei移动到编码器输出ze ( x )

1
2
3
4
5
z_q = torch.matmul(min_encodings, self.embedding.weight).view(z.shape)
        loss =  self.beta * torch.mean((z_q - z.detach()) ** 2))+torch.mean(((z_q.detach() - z) ** 2)
        z_q = z + (z_q - z).detach()
                                                # torch.mean((z_q-z.detach())**2) 可以更简单地写为
 F.mse_loss(z_q,z_e.detach())

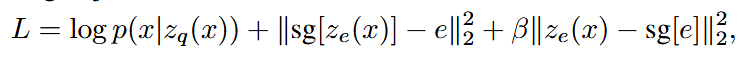
image-20241119192654741

此外可以使用EMA更新字典

image-20241119202801862

这里的更新逻辑是,每次更新ema_cluster_size,针对每个嵌入的向量,得到与它最近的特征向量个数,通过ema更新,而权重就是每次嵌入的值通过ema更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Update weights with EMA
       if self.training:
           self._ema_cluster_size = self._ema_cluster_size * self._decay + (
               1 - self._decay
           ) * torch.sum(encodings, 0)

           # Laplace smoothing
           n = torch.sum(self._ema_cluster_size.data)
           self._ema_cluster_size = (
               (self._ema_cluster_size + self._epsilon)
               / (n + self._n_embeddings * self._epsilon)
               * n
           )

           dw = torch.matmul(encodings.t(), flat_z_e)
           self._ema_w = nn.Parameter(
               self._ema_w * self._decay + (1 - self._decay) * dw
           )

           self._embedding.weight = nn.Parameter(
               self._ema_w / self._ema_cluster_size.unsqueeze(1)
           )

image-20241119222201269

VQVAE-2

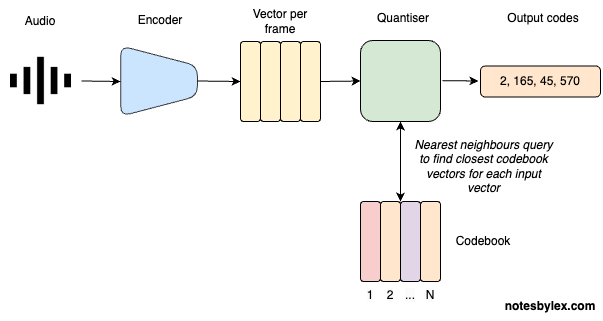
简单来说就是多尺度的vqvae,设计了多个encoder-codelayer-decoder.
首先特征通过多个encoder降维,得到不同尺度的特征,再将不同尺度特征进行quantize,quantize后得到的特征进行上采样再decoder最终得到多尺度特征. 此外论文也提出将codebook的维度从256到32,重建效果保持一致,同时将解码后的特征与codebook做l2-norm,使用cos相似度判断

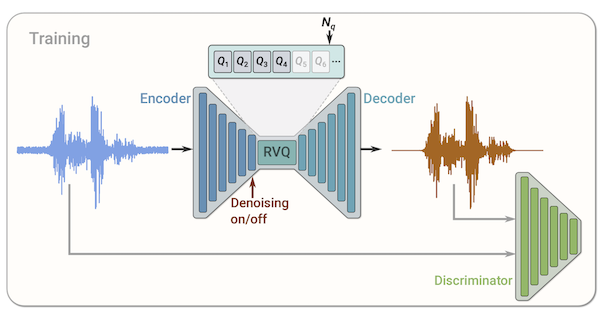
Residual VQ

道理非常简单——quantize(x-quantize(x-quantize(x-…)))

Vector Quantisation for Audio

SoundStream architecture

SIMVQ

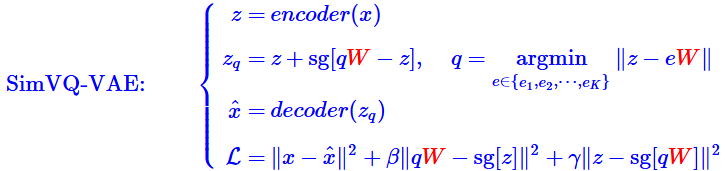
image-20241119222219261

据论文作者所说,在codebook上进行维度转换,提高编码表的利用率,使得在许多优化器上表现更好

可以看到上面代码中经常用到einops和einx以及torch的einsum操作,这些都是非常方便的库或者函数.这里介绍一下

einops中常用操作

image-20241119201935141

rearrange

最常用的就是rearrange了,可以用来转换axis的顺序,composition,decomposition等

1
2
3
4
5
6
7
8
9
x = torch.randn(10,20,10,10)
# order
y = rearrange(x,'b c h w -> b h w c')
print(y.shape)
# composition
y = rearrange(x,'b c h w -> b c (h w)')
# decomposition
y = rearrange(y,'b c (h w) -> b h w c')
y = rearrange(y,'(b1 b2) h w c -> b1 b2 h w c',b1=2)

reduce

1
2
# yet another example. Can you compute result shape?
reduce(ims, "(b1 b2) h w c -> (b2 h) (b1 w)", "mean", b1=2)

可以用于求均值,maxpooling等,

1
2
3
4
5
6
7
8
9
10
ims = torch.randn((10,20,30,30))*10-2
b,c,h,w = ims.shape
m_ims = reduce(ims,'b c h w -> b c',"min")
print(m_ims.shape)

m_ims = reduce(ims,'b c h w -> b (h w) c','min').transpose(1,2).reshape(b,c,h,w)
print(m_ims.shape)
print(ims == m_ims)
min2_ims = reduce(ims,'b c (h h2) (w w2) -> b c h w','mean',h2=2,w2=2)
reduce(ims,'b (h h2) (w w2) c -> h (b w) c',"max",h2=2,w2=2)

通过使用()保持dim,或者也可以使用1

1
2
3
4
5
6
7
data = torch.randn(10,20,30,40)
mean_ = reduce(data,'b c h w  -> b c () ()','mean') # 求均值
ans = data.mean(dim=[2,3],keepdim=True)
print((((ans-mean_)<1e-6).float()).mean())

max_pool = reduce(data,'b c (2 h) (2 w) -> b c h w','max') #max pooling
adaptive_max_pool = reduce(data,'b c h w -> b c ()','max')

stack and concatenation

1
2
3
4
5
6
# rearrange can also take care of lists of arrays with the same shape
x = list(ims)
print(type(x), "with", len(x), "tensors of shape", x[0].shape)
# that's how we can stack inputs
# "list axis" becomes first ("b" in this case), and we left it there
rearrange(x, "b h w c -> b h w c").shape

将一个列表的tensor中的列表大小维度进行转换

1
2
3
4
5
6
c = list()
c.append(torch.randn(10,20,30))
c.append(torch.randn(10,20,30))

rearrange(c,'l c h w -> c l h w').shape

或者求一个列表中的所有tensor和、max等

1
2
3
4
5
6
7
8
c = list()
c.append(torch.randn(10,20,30))
c.append(torch.randn(10,20,30))

rearrange(c,'l c h w -> c l h w').shape
reduce(c,'c l h w -> l h w','mean').shape
reduce(c,'c l h w -> l h w','sum').shape
reduce(c,'c l h w -> l h w','max').shape

add or remove axis

1
2
x = rearrange(x,'b h w c -> b 1 h w 1 c')
y = rearrange(y,'b h w c - b h (w c)')

channel shuffle

1
2
c = torch.randn(10,30,10,10)
rearrange(c,'b (g1 g2 c) h w -> b (g2 g1 c) h w',g1=3,g2=5).shape

repeat

1
2
3
repeat(x,'b h w c -> b (h 2) (w 2) c')
repeat(x,'h w c -> h new_axis w c',new_axis=5)
repeat(x,'h w c -> h 5 w c')

split dimension

1
2
3
c = torch.randn(10,30,10,10)
x,y,z = rearrange(c,'b (head c) h w -> head b c h w',head=3)
print(x.shape,y.shape,z.shape)

split有不同方法

1
2
3
y1, y2 = rearrange(x, 'b (split c) h w -> split b c h w', split=2)
result = y2 * sigmoid(y2) # or tanh
y1, y2 = rearrange(x, 'b (c split) h w -> split b c h w', split=2)
  • y1 = x[:, :x.shape[1] // 2, :, :]
  • y1 = x[:, 0::2, :, :]

striding anything

1
2
3
4
5
6
7
# each image is split into subgrids, each subgrid now is a separate "image"
y = rearrange(x, "b c (h hs) (w ws) -> (hs ws b) c h w", hs=2, ws=2)
y = convolve_2d(y)
# pack subgrids back to an image
y = rearrange(y, "(hs ws b) c h w -> b c (h hs) (w ws)", hs=2, ws=2)

assert y.shape == x.shape

可以看到最常用的函数就是rearrange,reduce以及repeat,基本替代了原本的sum,transpose,expand,reshape等torch操作

parse_shape

通过parse_shape,相当于更方便地获得了需要的维度大小

1
2
y = np.zeros([700])
rearrange(y, '(b c h w) -> b c h w', **parse_shape(x, 'b _ h w')).shape

pack and unpack

pack是将一些列数据中的的一些维度放在一起

1
2
3
4
5
6
h,w = 100,200
import numpy as np
img_rgb = np.random.random([h,w,3])
img_depth = np.random.random([h,w])
img_rgbd,ps = pack([img_rgb,img_depth],'h w *')
print(img_rgbd.shape,ps)
1
2
unpacked_rgb,unpacked_depth = unpack(img_rgbd,ps,"h w *")
print(unpacked_rgb.shape,unpacked_depth.shape)

结合torch使用layers

1
from einops.layers.torch import Rearrange,Reduce

Einx

一种类似torch.einsum的计算方式,einsumeinsum tutorial是一种方便计算多个tensor乘积的方式,而Einx方便了写MLP-based架构代码,通过weight_shape和bias_shape结合pattern构造mlp

1
2
3
4
from einops.layers.torch import EinMix as Mix
mlp = Mix('t b c-> t b c_out',weight_shape='c c_out',c=10,c_out=20)
x = torch.randn(10,30,10)
y = mlp(x)

值得一提的是,einops也有einsum

1
2
3
4
from einops import einsum, pack, unpack
# einsum is like ... einsum, generic and flexible dot-product
# but 1) axes can be multi-lettered  2) pattern goes last 3) works with multiple frameworks
C = einsum(A, B, 'b t1 head c, b t2 head c -> b head t1 t2')

相关资料

  1. MishaLaskin/vqvae: A pytorch implementation of the vector quantized variational autoencoder (https://arxiv.org/abs/1711.00937)
  2. VQ-VAE/vq_vae/auto_encoder.py at master · nadavbh12/VQ-VAE
  3. VQ-VAE/vqvae.py at main · AndrewBoessen/VQ-VAE
  4. vqvae-2/vqvae.py at main · vvvm23/vqvae-2
  5. Autoregressive Models in Deep Learning — A Brief Survey | George Ho
  6. lucidrains/vector-quantize-pytorch: Vector (and Scalar) Quantization, in Pytorch
  7. VQ-VAE的简明介绍：量子化自编码器 - 科学空间|Scientific Spaces
  8. VQ的旋转技巧：梯度直通估计的一般推广 - 科学空间|Scientific Spaces
  9. VQ的又一技巧：给编码表加一个线性变换 - 科学空间|Scientific Spaces
  10. Writing better code with pytorch+einops
  11. Residual Vector Quantisation - Notes by Lex
  12. rese1f/Awesome-VQVAE: A collection of resources and papers on Vector Quantized Variational Autoencoder (VQ-VAE) and its application
-------------本文结束感谢您的阅读-------------
相关文章
感谢阅读.

欢迎关注我的其它发布渠道